承接自经典算法 的笔记。
1.树状数组
又名fenwickTree,国内又名BinaryIndexTree(名称很形象,与二进制有关)。树状数组无法解决RMQ问题,因为区间不可重复贡献,能解决的问题有:单点修改-区间求和、区间修改-区间求和、逆序对问题。
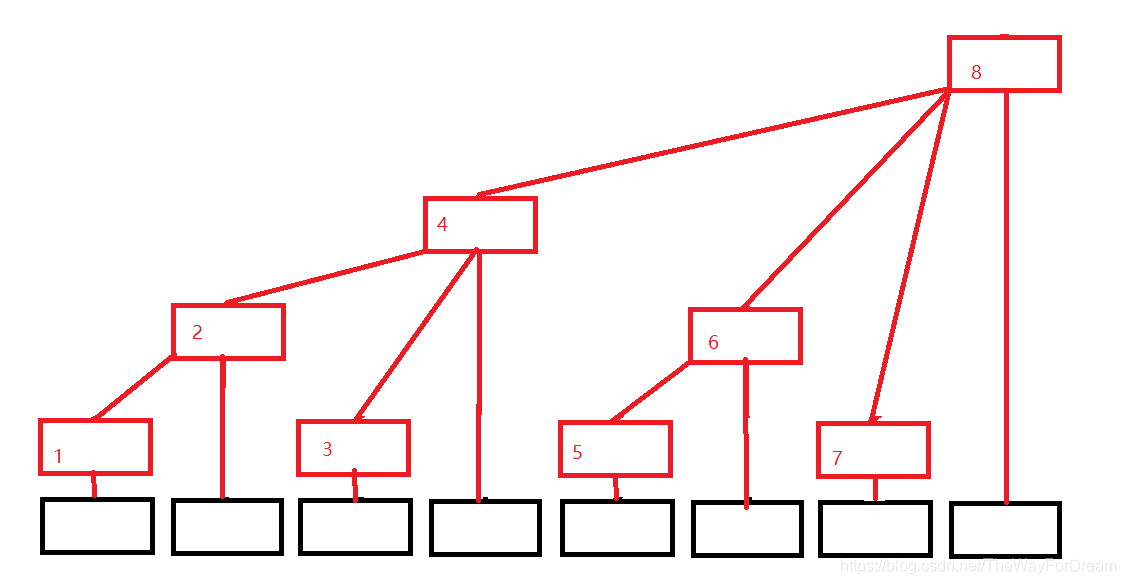
树状数组中每一个位置都是保存的一段区间的和。对原数组某一个下标x加上一个值,会影响到树状数组中该下标x,以及该下标x+lowbit(x)的位置,一直到最后一位。如图,红色值为树状数组的下标,例如下标8处的值,等于其所有子类的相加的和:p r e S u m [ 8 ] = p r e S u m [ 4 ] + p r e S u m [ 6 ] + p r e S u m [ 7 ] + n u m s [ 8 ] preSum[8] = preSum[4] + preSum[6] + preSum[7] + nums[8] p r e S u m [ 8 ] = p r e S u m [ 4 ] + p r e S u m [ 6 ] + p r e S u m [ 7 ] + n u m s [ 8 ]
如果对原数组下标为5加上1,则如下二叉树部分,对下标为5的加上1,再对5+lowbit(5) = 6下标加上1,再对6 + lowbit(6) = 8下标加上1,接下来会超过数组边界,所以停止操作。
如果求区间[x, y]的值,则可以转化为求区间[1, y] - [1, x - 1]的值。我们从树状数组上往下查,假设要查[1, 6]的值,先查树状数组中6的值,在查6-lowbit(6) = 4 的值,接着4-lowbit(4) = 0,超出操作范围,停止操作。将这两者值相加的到区间[1, 6]的值。
1.单点修改-区间求和
模板题:P3374 【模板】树状数组 1 - 洛谷
如题,已知一个数列,你需要进行下面两种操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 import java.io.*;import java.util.StringTokenizer;public class Main { private static int [] prevSumArr; public static void main (String[] args) throws IOException { PrintWriter pw = new PrintWriter (new BufferedWriter (new OutputStreamWriter (System.out))); int n = rd.nextInt(); int m = rd.nextInt(); prevSumArr = new int [n + 1 ]; for (int i = 1 ; i <= n; i++) { int v = rd.nextInt(); add(i, v); } for (int i = 0 ; i < m; i++) { int a = rd.nextInt(); int x = rd.nextInt(); int y = rd.nextInt(); if (a == 1 ) { add(x, y); } else { pw.println(ask(x, y)); } } pw.flush(); } public static void add (int x, int v) { for (; x <= prevSumArr.length - 1 ; x += (x & -x)) { prevSumArr[x] += v; } } public static int ask (int x) { int ans = 0 ; for (; x > 0 ; x -= (x & -x)) { ans += prevSumArr[x]; } return ans; } public static int ask (int x, int y) { return ask(y) - ask(x - 1 ); } static class rd { static BufferedReader reader = new BufferedReader (new InputStreamReader (System.in)); static StringTokenizer tokenizer = new StringTokenizer ("" ); static String nextLine () throws IOException { return reader.readLine(); } static String next () throws IOException { while (!tokenizer.hasMoreTokens()) { tokenizer = new StringTokenizer (reader.readLine()); } return tokenizer.nextToken(); } static int nextInt () throws IOException { return Integer.parseInt(next()); } static double nextDouble () throws IOException { return Double.parseDouble(next()); } static long nextLong () throws IOException { return Long.parseLong(next()); } } }
2.区间修改-单点求值
模板题:P3368 【模板】树状数组 2 - 洛谷
把原数组先进行差分,再以此创建树状数组。则对原数组[x, y] 处加1,则变成对差分数组下标x处加1,下标y+1处-1。(若y=n,y+1则会超过树状数组最大下标n越界,会有问题吗?不会,因为add的时候限制了小于n,不会导致越界,丢弃掉差分数组越界那一部分,对差分数组还原无影响)
如题,已知一个数列,你需要进行下面两种操作:
将某区间每一个数加上x ;
求出某一个数的值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 import java.io.*;import java.util.StringTokenizer;public class Main { private static int [] prevSumArr; public static void main (String[] args) throws IOException { PrintWriter pw = new PrintWriter (new BufferedWriter (new OutputStreamWriter (System.out))); int n = Rd.nextInt(); int m = Rd.nextInt(); prevSumArr = new int [n + 1 ]; int last = 0 ; for (int i = 1 ; i <= n; i++) { int v = Rd.nextInt(); add(i, v - last); last = v; } for (int i = 0 ; i < m; i++) { int a = Rd.nextInt(); if (a == 1 ) { int x = Rd.nextInt(); int y = Rd.nextInt(); int v = Rd.nextInt(); add(x, y, v); } else { int x = Rd.nextInt(); pw.println(ask(x)); } } pw.flush(); } public static void add (int x, int v) { for (; x <= prevSumArr.length - 1 ; x += (x & -x)) { prevSumArr[x] += v; } } public static void add (int x, int y, int v) { add(x, v); add(y + 1 , -v); } public static int ask (int x) { int ans = 0 ; for (; x > 0 ; x -= (x & -x)) { ans += prevSumArr[x]; } return ans; } public static int ask (int x, int y) { return ask(y) - ask(x - 1 ); } static class Rd { static BufferedReader reader = new BufferedReader (new InputStreamReader (System.in)); static StringTokenizer tokenizer = new StringTokenizer ("" ); static String nextLine () throws IOException { return reader.readLine(); } static String next () throws IOException { while (!tokenizer.hasMoreTokens()) { tokenizer = new StringTokenizer (reader.readLine()); } return tokenizer.nextToken(); } static int nextInt () throws IOException { return Integer.parseInt(next()); } static double nextDouble () throws IOException { return Double.parseDouble(next()); } static long nextLong () throws IOException { return Long.parseLong(next()); } } }
3.逆序对问题
模板题:LCR 170. 交易逆序对的总数 - 力扣(LeetCode)
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
此题目,除了使用分治算法外,还可以使用树状数组求解。
首先,对原数组nums进行离散化,这里使用排序,排序后得到数组sortArr,就知道每个数离散后的下标。然后按照从左到右的顺序遍历原数组nums,遍历到数num的时候,查找数num在sortArr中最小的下标left和最大right的下标,查找树装数组中比num大的数(即大于right计数)即为答案。然后在left+1计数1,表示添加了一个数num。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 class Solution { private int [] tree; public int reversePairs (int [] record) { this .tree = new int [record.length + 1 ]; int [] sortArr = Arrays.copyOf(record, record.length); Arrays.sort(sortArr); int ans = 0 ; for (int i = 0 ; i < record.length; i++) { int v = record[i]; int left = binLeftSearch(sortArr, v); int right = binRightSearch(sortArr, v); ans += ask(right + 2 , tree.length - 1 ); add(left + 1 , 1 ); } return ans; } private int binRightSearch (int [] sortArr, int v) { int left = 0 ; int right = sortArr.length - 1 ; while (left < right) { int mid = left + right + 1 >> 1 ; if (sortArr[mid] <= v) { left = mid; } else { right = mid - 1 ; } } return left; } private int binLeftSearch (int [] sortArr, int v) { int left = 0 ; int right = sortArr.length - 1 ; while (left < right) { int mid = left + right >> 1 ; if (check(sortArr, mid, v)) { right = mid; } else { left = mid + 1 ; } } return left; } private boolean check (int [] sortArr, int mid, int v) { return sortArr[mid] >= v; } public void add (int x, int v) { for (; x < tree.length; x += x & (-x)) { tree[x] += v; } } public int ask (int x) { int ans = 0 ; for (; x >= 1 ; x -= x & (-x)) { ans += tree[x]; } return ans; } public int ask (int x, int y) { return ask(y) - ask(x - 1 ); } }
2.线段树
之前在经典算法 中写过线段树的笔记,所以你知道我拖延了多久了吧(懒癌晚期实锤),那段笔记只记叙了单点修改,区间查询。
1.区间修改-区间查询
模板题目:P3372 【模板】线段树 1 - 洛谷
如题,已知一个数列,你需要进行下面两种操作:
将某区间每一个数加上 k 。
求出某区间每一个数的和。
如果区间修改时,逐个去修改,单独的修改部分就会O ( N 2 l g N ) O(N^2lgN) O ( N 2 l g N )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 import java.io.*;import java.math.BigInteger;import java.util.StringTokenizer;public class Main { private static long [] nums; private static TreeNode[] tree; private static int n; public static void main (String[] args) throws IOException { Fr sc = new Fr (); PrintWriter pw = new PrintWriter (new BufferedOutputStream (System.out)); int n = sc.nextInt(); int m = sc.nextInt(); tree = new TreeNode [n * 4 ]; nums = new long [n]; for (int i = 0 ; i < n; i++) { nums[i] = sc.nextInt(); } build(0 , n - 1 , 1 ); for (int i = 0 ; i < m; i++) { int op = sc.nextInt(); int x = sc.nextInt() - 1 ; int y = sc.nextInt() - 1 ; if (op == 1 ) { int k = sc.nextInt(); change(x, y, k, 1 ); } else { long ans = ask(x, y, 1 ); pw.println(ans); } } pw.flush(); } private static long ask (int left, int right, int p) { if (left <= tree[p].left && tree[p].right <= right) { return tree[p].sum; } pushDown(p); int mid = tree[p].left + tree[p].right >> 1 ; long ans = 0 ; if (left <= mid) { ans += ask(left, right, p * 2 ); } if (right > mid) { ans += ask(left, right, p * 2 + 1 ); } return ans; } private static void change (int left, int right, int val, int p) { if (left <= tree[p].left && tree[p].right <= right) { tree[p].sum += (long ) val * (tree[p].right - tree[p].left + 1 ); tree[p].lazy += val; return ; } pushDown(p); int mid = tree[p].left + tree[p].right >> 1 ; if (left <= mid) { change(left, right, val, p * 2 ); } if (right > mid) { change(left, right, val, p * 2 + 1 ); } pushUp(p); } private static void build (int left, int right, int p) { tree[p] = new TreeNode (left, right); if (left == right) { tree[p].sum = nums[left]; return ; } int mid = left + right >> 1 ; build(left, mid, p * 2 ); build(mid + 1 , right, p * 2 + 1 ); pushUp(p); } private static void pushDown (int p) { if (tree[p].lazy != 0 ) { tree[p * 2 ].sum += tree[p].lazy * (tree[p * 2 ].right - tree[p * 2 ].left + 1 ); tree[p * 2 + 1 ].sum += tree[p].lazy * (tree[p * 2 + 1 ].right - tree[p * 2 + 1 ].left + 1 ); tree[p * 2 ].lazy += tree[p].lazy; tree[p * 2 + 1 ].lazy += tree[p].lazy; tree[p].lazy = 0 ; } } private static void pushUp (int p) { tree[p].sum = tree[p * 2 ].sum + tree[p * 2 + 1 ].sum; } static class TreeNode { public int left; public int right; public long sum; public long lazy = 0 ; public TreeNode () { } public TreeNode (int left, int right) { this .left = left; this .right = right; } public TreeNode (int left, int right, int sum) { this .left = left; this .right = right; this .sum = sum; } } static class Fr { static BufferedReader reader = new BufferedReader (new InputStreamReader (System.in)); static StringTokenizer tokenizer = new StringTokenizer ("" ); static String nextLine () throws IOException { return reader.readLine(); } static String next () throws IOException { while (!tokenizer.hasMoreTokens()) { tokenizer = new StringTokenizer (reader.readLine()); } return tokenizer.nextToken(); } static int nextInt () throws IOException { return Integer.parseInt(next()); } static double nextDouble () throws IOException { return Double.parseDouble(next()); } static long nextLong () throws IOException { return Long.parseLong(next()); } static BigInteger nextBigInteger () throws IOException { return new BigInteger (Fr.nextLine()); } } }
2.乘法-加法操作
模板题:P3373 【模板】线段树 2 - 洛谷
如题,已知一个数列,你需要进行下面三种操作:
将某区间每一个数乘上 x ;
将某区间每一个数加上 x ;
求出某区间每一个数的和。
同时包含多个操作时,会有优先级关系,具体的我也不懂,先把模板记着。区间修改的lazy是代表的加法懒标记,现在懒标记具体为加法add,乘法mul。add初始化为0,mul初始化为1。(0加任何数等于其本身,1乘以任何数等于其本身)。乘法的优先级高于加法,所以下移操作,先乘法计算,后加法计算。同时乘法操作(mul方法)时,要把加法计算补上
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 import java.io.*;import java.util.StringTokenizer;public class Main { private static long [] nums; private static TreeNode[] trees; private static long m; public static void main (String[] args) throws IOException { Fr sc = new Fr (); PrintWriter pw = new PrintWriter (new BufferedOutputStream (System.out)); int n = sc.nextInt(); int q = sc.nextInt(); m = sc.nextInt(); nums = new long [n]; trees = new TreeNode [n << 2 ]; for (int i = 0 ; i < n; i++) { nums[i] = sc.nextInt(); } build(0 , nums.length - 1 , 1 ); for (int i = 0 ; i < q; i++) { int type = sc.nextInt(); int x = sc.nextInt() - 1 ; int y = sc.nextInt() - 1 ; if (type == 2 ) { int k = sc.nextInt(); add(x, y, k, 1 ); } else if (type == 1 ) { int k = sc.nextInt(); mul(x, y, k, 1 ); } else { pw.println(ask(x, y, 1 ) % m); } } pw.flush(); } public static void build (int left, int right, int p) { trees[p] = new TreeNode (left, right); if (left == right) { trees[p].sum = nums[left] % m; return ; } int mid = left + right >> 1 ; build(left, mid, p * 2 ); build(mid + 1 , right, p * 2 + 1 ); pushUp(p); } public static void add (int left, int right, int val, int p) { if (left <= trees[p].left && trees[p].right <= right) { trees[p].sum = (trees[p].sum + (long ) (trees[p].right - trees[p].left + 1 ) * val) % m; trees[p].add = (trees[p].add + val) % m; return ; } pushDown(p); int mid = trees[p].left + trees[p].right >> 1 ; if (left <= mid) { add(left, right, val, p * 2 ); } if (right > mid) { add(left, right, val, p * 2 + 1 ); } pushUp(p); } public static void mul (int left, int rihgt, int val, int p) { if (left <= trees[p].left && trees[p].right <= rihgt) { trees[p].sum = (trees[p].sum * val) % m; trees[p].mul = (trees[p].mul * val) % m; trees[p].add = (trees[p].add * val) % m; return ; } pushDown(p); int mid = trees[p].left + trees[p].right >> 1 ; if (left <= mid) { mul(left, rihgt, val, p * 2 ); } if (rihgt > mid) { mul(left, rihgt, val, p * 2 + 1 ); } pushUp(p); } public static long ask (int left, int right, int p) { if (left <= trees[p].left && trees[p].right <= right) { return trees[p].sum; } pushDown(p); long ans = 0 ; int mid = trees[p].left + trees[p].right >> 1 ; if (left <= mid) { ans = (ans + ask(left, right, p * 2 )) % m; } if (mid < right) { ans = (ans + ask(left, right, p * 2 + 1 ) % m); } return ans; } private static void pushDown (int p) { trees[p * 2 ].sum = (trees[p * 2 ].sum * trees[p].mul + trees[p].add * (trees[p * 2 ].right - trees[p * 2 ].left + 1 )) % m; trees[p * 2 ].mul = (trees[p * 2 ].mul * trees[p].mul) % m; trees[p * 2 ].add = (trees[p * 2 ].add * trees[p].mul + trees[p].add) % m; trees[p * 2 + 1 ].sum = (trees[p * 2 + 1 ].sum * trees[p].mul + trees[p].add * (trees[p * 2 + 1 ].right - trees[p * 2 + 1 ].left + 1 )) % m; trees[p * 2 + 1 ].mul = (trees[p * 2 + 1 ].mul * trees[p].mul) % m; trees[p * 2 + 1 ].add = (trees[p * 2 + 1 ].add * trees[p].mul + trees[p].add) % m; trees[p].mul = 1 ; trees[p].add = 0 ; } private static void pushUp (int p) { trees[p].sum = (trees[p * 2 ].sum + trees[p * 2 + 1 ].sum) % m; } public static class TreeNode { public int left; public int right; public long sum; public long add = 0 ; public long mul = 1 ; public TreeNode (int left, int right) { this .left = left; this .right = right; } } public static class Fr { BufferedReader reader = new BufferedReader (new InputStreamReader (System.in)); StringTokenizer tokenizer = new StringTokenizer ("" ); String nextLine () throws IOException { return reader.readLine(); } String next () throws IOException { while (!tokenizer.hasMoreTokens()) { tokenizer = new StringTokenizer (reader.readLine()); } return tokenizer.nextToken(); } int nextInt () throws IOException { return Integer.parseInt(next()); } double nextDouble () throws IOException { return Double.parseDouble(next()); } long nextLong () throws IOException { return Long.parseLong(next()); } } }
3.最小生成树
介绍参见:最小生成树_百度百科
n个点,这些点之间有一些有权边,请通过这些有权边,将这n个点连接起来,使得所有点都被连接在一起(即能任意一点到达其他所有的点)。其中满足条件的边权和的最小值的情况,就是最小生成树。
假设有n个点,m条边。最小生成树一点只有n-1条连接边。且不会成环。
1.kruskal算法
该算法的思想是选边,每次都选之前未被选择的最小的边。查看该边是与之前选择的边构成环,如果成环则丢弃该边。否则选择这条边。直到选择了n-1条边,就构成了最小生成树。这里采用排序后,使用并查集的方式查询是否成环。
排序所有边。
选择最小的未被选择的边。如果不与之前选择的边成环,则选择,否则丢弃
重复2步骤直到选择了n-1条边。
时间复杂度 :O(mlogm),m条边,并查集logm(只采用了路径压缩),适用于稀疏图。
另外如果先选最大的,就是最大生成树 了,
模板题:1584. 连接所有点的最小费用 - 力扣
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 class Solution { public int minCostConnectPoints (int [][] points) { int n = points.length; List<Edge> edges = new ArrayList <>(); for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n; j++) { if (i != j) { int dis = Math.abs(points[i][0 ] - points[j][0 ]) + Math.abs(points[i][1 ] - points[j][1 ]); edges.add(new Edge (i, j, dis)); } } } kruskals(edges, n); return ans; } private List<Edge> minDisList; private int ans = 0 ; public void kruskals (List<Edge> edges, int n) { this .minDisList = new ArrayList <>(); Collections.sort(edges, (a, b) -> a.w - b.w); DSU dsu = new DSU (n); for (Edge edge : edges) { int u = edge.u; int v = edge.v; int w = edge.w; if (!dsu.isUnion(u, v)) { dsu.union(u, v); ans += w; minDisList.add(new Edge (u, v, w)); } } } static class Edge { public int u; public int v; public int w; public Edge (int u, int v, int w) { this .u = u; this .v = v; this .w = w; } @Override public String toString () { return "Edge{" + "u=" + u + ", v=" + v + ", w=" + w + '}' ; } } public static class DSU { public int setCount; public int [] fa; public DSU (int n) { this .fa = new int [n]; this .setCount = n; for (int i = 0 ; i < fa.length; i++) { fa[i] = i; } } public boolean isUnion (int x, int y) { return findFa(x) == findFa(y); } public int findFa (int x) { if (fa[x] == x) { return x; } int rootFa = findFa(this .fa[x]); fa[x] = rootFa; return rootFa; } public void union (int x, int y) { int xFa = findFa(x); int yFa = findFa(y); if (xFa != yFa) { setCount--; } fa[xFa] = yFa; } } }
2.prim算法
该算法的思想是选点,先选定一个点1(一般为编号最小的点),加入到选中集合A,未选中的点存在集合B。接着从集合B中的所有点找到距离集合A中任意点距离(权重)最近的点,假设为点3,将3加入集合A,现在集合A中有点1和3。接着再从集合B中的所有点找出一个点,距离集合A中的1或3距离(权重)最近的点。直到所有的点都被加入到集合A。
选择编号最小的点从集合B加入集合A
从B中选择一个点,该点距离集合A中的某个点是距离最近的
重复2步骤直到所有点被从集合B加入集合A
时间复杂度:O ( n 2 ) O(n^2) O ( n 2 )
模板题:1584. 连接所有点的最小费用 - 力扣
注意点编号是从1开始还是从0开始,这里题目没说,默认从0开始,但是模板是从1开始的,所以略有改动。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 class Solution { private int [] minDisArr; private int [] fa; private int INF = 0x3f3f3f3f ; public int minCostConnectPoints (int [][] points) { int n = points.length; int [][] graphArr = new int [points.length + 1 ][points.length + 1 ]; for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n; j++) { if (i != j) { graphArr[i + 1 ][j + 1 ] = Math.abs(points[i][0 ] - points[j][0 ]) + Math.abs(points[i][1 ] - points[j][1 ]); } } } this .minDisArr = new int [n + 1 ]; Arrays.fill(minDisArr, INF); boolean [] vis = new boolean [n + 1 ]; fa = new int [n + 1 ]; minDisArr[1 ] = 0 ; fa[1 ] = -1 ; for (int i = 1 ; i <= n; i++) { int u = findMin(vis, minDisArr); vis[u] = true ; for (int v = 1 ; v <= n; v++) { if (!vis[v] && graphArr[u][v] < minDisArr[v]) { minDisArr[v] = graphArr[u][v]; fa[v] = u; } } } for (int i = 1 ; i < minDisArr.length; i++) { if (minDisArr[i] == INF) { return -1 ; } } int ans = 0 ; for (int i = 1 ; i < minDisArr.length; i++) { ans += minDisArr[i]; } return ans; } private int findMin (boolean [] vis, int [] minDisArr) { int minDis = INF; int minIdx = -1 ; for (int i = 1 ; i < minDisArr.length; i++) { if (!vis[i] && minDisArr[i] < minDis) { minDis = minDisArr[i]; minIdx = i; } } return minIdx; } }
4.N叉树的最近公共祖先
1.倍增
倍增法主要基于1、2两点。
任何一个10进制数能用二进制表示,进而能够被k(这里k指任意数量)个2的幂次相加得到,后面的数的下标表示进制。5 10 5_{10} 5 1 0 10 1 2 101_2 1 0 1 2 10 0 2 + 1 2 100_2 + 1_2 1 0 0 2 + 1 2 4 10 、 1 10 4_{10}、1_{10} 4 1 0 、 1 1 0
若memeArr[i][j]的值表示从节点i跳2^j步到的节点编号,则有m e m e A r r [ i ] [ j ] = m e m e A r r [ [ m e m e A r r [ i ] [ j − 1 ] ] ] [ j − 1 ] memeArr[i][j] = memeArr[[memeArr[i][j-1]]][j-1] m e m e A r r [ i ] [ j ] = m e m e A r r [ [ m e m e A r r [ i ] [ j − 1 ] ] ] [ j − 1 ] memeArr[i][0],表示从编号i的节点跳2^0步到达节点(即跳一步,到达节点i父节点)。
将两个节点跳到同一高度后,我们倍增的去跳到最近公共祖先的子节点。再往上跳一步就是最近公共祖先。
时间复杂度:预处理LCA为O(n),对于m此询问,每次询问为O(lgn),因此总的为O(n + mlgn)。
模板题:P3379 【模板】最近公共祖先(LCA)
另有LC模板题目:236. 二叉树的最近公共祖先 ,此题暴力也可过,是O(N)的时间复杂度,先建立到父节点反向节点记录,然后将深度更深的那个点跳到两个节点一样深,然后一起往上一直跳,直到两个节点是同一个节点,即为答案。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 import java.io.*;import java.util.*;public class Main { private static int n; private static int h; private static int [][] memeArr; private static int [] deepArr; public static void main (String[] args) throws IOException { Fr sc = new Fr (); PrintWriter pw = new PrintWriter (new BufferedOutputStream (System.out)); n = sc.nextInt(); int m = sc.nextInt(); int s = sc.nextInt(); List<Integer>[] graphListArr = new List [n + 1 ]; Arrays.setAll(graphListArr, x -> new ArrayList <>()); for (int i = 1 ; i <= n - 1 ; i++) { int x = sc.nextInt(); int y = sc.nextInt(); graphListArr[x].add(y); graphListArr[y].add(x); } initLca(s, graphListArr); for (int i = 0 ; i < m; i++) { int a = sc.nextInt(); int b = sc.nextInt(); int ans = lca(a, b); pw.println(ans); } pw.flush(); } public static void initLca (int s, List<Integer>[] graphListArr) { h = (int ) (Math.log(n) / Math.log(2 )) + 1 ; deepArr = new int [n + 1 ]; memeArr = new int [n + 1 ][h + 1 ]; Deque<Integer> queue = new ArrayDeque <>(); queue.add(s); deepArr[s] = 1 ; Arrays.fill(memeArr[s], s); while (!queue.isEmpty()) { int u = queue.pollFirst(); for (Integer v : graphListArr[u]) { if (deepArr[v] != 0 ) { continue ; } deepArr[v] = deepArr[u] + 1 ; memeArr[v][0 ] = u; for (int i = 1 ; i <= h; i++) { memeArr[v][i] = memeArr[memeArr[v][i - 1 ]][i - 1 ]; } queue.addLast(v); } } } public static int lca (int x, int y) { if (deepArr[x] > deepArr[y]) { int temp = x; x = y; y = temp; } for (int i = h; i >= 0 ; i--) { if (deepArr[memeArr[y][i]] >= deepArr[x]) { y = memeArr[y][i]; } } if (x == y) { return x; } for (int i = h; i >= 0 ; i--) { if (memeArr[x][i] != memeArr[y][i]) { x = memeArr[x][i]; y = memeArr[y][i]; } } return memeArr[x][0 ]; } static class Fr { BufferedReader reader = new BufferedReader (new InputStreamReader (System.in)); StringTokenizer tokenizer = new StringTokenizer ("" ); String nextLine () throws IOException { return reader.readLine(); } String next () throws IOException { while (!tokenizer.hasMoreTokens()) { tokenizer = new StringTokenizer (reader.readLine()); } return tokenizer.nextToken(); } int nextInt () throws IOException { return Integer.parseInt(next()); } double nextDouble () throws IOException { return Double.parseDouble(next()); } long nextLong () throws IOException { return Long.parseLong(next()); } } }
补充1:对于树上任意两点的距离,deepArr[x] + deepArr[y] - (2 * deepArr[lca(x, y)]);,根节点到x节点的距离deepArr[x] - 1,到y节点的距离deepArr[y]-1,此两者相加,就是(根到最近公共祖先节点 * 2 + 公共祖先节点到x节点 + 公共祖先节点到y节点),将根节点到公共祖节点的两次减去即可。根到公共祖先节点的距离deepArr[lca(x, y)] - 1。所以有
( d e e p A r r [ x ] − 1 ) + ( d e e p A r r [ y ] − 1 ) − 2 ∗ ( d e e p A r r [ l c a ( x , y ) ] − 1 ) = d e e p A r r [ x ] + d e e p A r r [ y ] − ( 2 ∗ d e e p A r r [ l c a ( x , y ) ] ) (deepArr[x] - 1) + (deepArr[y]-1) - 2*(deepArr[lca(x, y)] - 1) = deepArr[x] + deepArr[y] - (2 * deepArr[lca(x, y)])
( d e e p A r r [ x ] − 1 ) + ( d e e p A r r [ y ] − 1 ) − 2 ∗ ( d e e p A r r [ l c a ( x , y ) ] − 1 ) = d e e p A r r [ x ] + d e e p A r r [ y ] − ( 2 ∗ d e e p A r r [ l c a ( x , y ) ] )
因此计算任意两节点的最短距离代码为(需要initLca方法前置处理):
1 2 3 int clac (int x, int y) { return deepArr[x] + deepArr[y] - (2 * deepArr[lca(x, y)]); }
补充2:对于加权图树上任意两点距离
2.TarjanLCA
// TODO暂时留坑