Songbirds


春

前缀和与差分

  • ~9.00K 字
  1. 1. 一维前缀和
    1. 1.1. 模板题：
  2. 2. 一维差分
    1. 2.1. 模板题：
  3. 3. 二维前缀和
    1. 3.1. 模板题：
  4. 4. 二维差分
    1. 4.1. 模板题

差分与前缀和

一维前缀和

对于一个长度为n的数组nums，其下标i处的前缀和 = 从下标0到下标i的值累加得到的新值。这些新值重新组成一个新的数组，称为前缀和数组。我们一般说的前缀和特指前缀和数组，这里为了说明清晰还是区分前缀和与前缀和数组。另外为了方便计算与还原数组，我习惯添加一个前置0，形成长度为n+1的前缀和数组。

一维差分

对于一个长度为n的数组nums，其下标i处的差分=下标i处的值-下标i-1处的值。这些新值组成的新的数组称为差分数组，对于下标0处的值，没有对象可以减去，因此维持不变。同理本笔记也区分差分和差分数组。另外为了方便计算与还原数组，我习惯给差分数组最后加一个0-nums[n-1]的值，相当于给原数组nums添加了一个0的值形成长度为n+1的nums数组

一维前缀和

一维前缀和公式可以总结如下，对于下标i处的元素sum[i]有：(注意长为n的数组nums下标从0开始，到n-1结束)

sum[n]=∑i=0n−1nums[i]sum[n]=\sum_{i=0}^{n-1}nums[i]

所以一维前缀和数组可以表示为：sumArr = [0,sum[0],sum[1],sum[2]…sum[n-1]]。（加了前置0）

前缀和的应用：前缀和主要应用于多次快速求解数组nums区间[L,R]的和。当我们预处理得到前缀和数组sumArr后，

sum[R+1]−sum[L]sum[R+1]-sum[L]

就是nums区间[L,R]的所有值的和。因为sum[R+1]是nums下标0到下标R的数的和，sum[L]是下标0到下标L-1的和。（注意：因为我的习惯添加了前置0到sumArr数组，所以原nums数组对应到sumArr数组需要加1）。两者相减就是答案。

模板题：

给你一个长度为n的数组nums，再给你一个m行2列的二维数组querys表示m次询问，每个子数组包含两个数字L、R，表示查询nums中L到R所有数之和。
数据范围：1 <= n <= 10510^5，1 <= m <= 10510^5，0 <= L <= R <= n - 1。

分析：朴素的做法是对于每次querys[i]，遍历L到R的数组，然后累加得到结果即可，分析可知时间复杂度为O(1010)O(10^{10})。显然是不符合题目要求的。但是使用前缀和可以达到O(105)O(10^{5})的时间复杂度，即query次数的时间。符合题目要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int[] prefixSum(int[] nums, int[][] querys) {
    int[] sumArr = new int[nums.length + 1];
    // 前缀和
    for (int i = 0; i < nums.length; i++) {
        sumArr[i + 1] = sumArr[i] + nums[i];
    }
    int[] ansArr = new int[querys.length];
    for (int i = 0; i < querys.length; i++) {
        int left = querys[i][0];
        int right = querys[i][1];
        // 求left到right的元素的和
        ansArr[i] = sumArr[right + 1] - sumArr[left];
    }
    return ansArr;
}
1
2
3
一组测试用例
int[] nums = {1, 2, 3, 4, 5};
int[][] querys = {{1, 3}, {2, 4}, {0, 4}};

一维差分

一维差分的公式可以总结如下，对于下标i处的元素diff[i]有：

diff[i]=nums[i]−nums[i−1]diff[i] = nums[i] - nums[i - 1]

所以一维差分数组可以表示为：sumArr = [diff[0], diff[1], diff[2]…diff[n-1], 0]。（加了后置0）

一维差分的应用：差分主要和前缀和一起搭配使用，先使用差分，处理区间加上一个数，或减去一个数的逻辑，然后使用前缀和，还原整个数组。

例如，对于一个长度为5数组nums={a1, a2, a3, a4, a5}；先求出其差分数组，补上后置0（个人习惯），得到diffArr = {a1, a2 - a1, a3 - a2, a4 - a3, a5 - a4, 0}。

假设对nums的区间1到3加上一个数x，相当于对于nums的1下标加上x，在3+1下标上减去x。得到diffArr = {a1, a2 - a1 + x, a3 - a2, a4 - a3, a5 -a4 - x, 0}。(我们使用前缀和可以将diffArr其还原到newNums = {a1, a2 + x, a3 + x, a4 + x, a5, 0}。)。

再次对nums区间0到4减去一个数y，相当于对于nums的0的下标减去y，在4+1下标上加上y，得到diffArr = {a1 - y, a2 - a1 + x, a3 - a2, a4 - a3, a5 - a4 - x, y}，使用前缀和，还原可得到newNums = {a1 - y, a2 + x - y, a3 + x - y, a4 + x - y, a5 - y, a5}。在diffArr中下标0到4的5个元素就是最终的答案。

模板题：

给你一个长度为n的数组nums，再给你一个m行4列的二维数组opers表示m次操作，每个子数组包含两个数字oper、L、R、num。oper=0或1，0表示对于L、R的连续区间加上num，1表示对于L、R的连续区间减去num。所有操作后，求最终的数组。
数据范围：1 <= n <= 10510^5，1 <= m <= 10510^5，oper=1或2，0 <= L <= R <= n - 1。

分析：朴素的做法是对于每次opers[i]，遍历L到R的数组，然后操作得到结果即可，分析可知时间复杂度为O(1010)O(10^{10})。显然是不符合题目要求的。但是使用差分可以达到O(105)O(10^{5})的时间复杂度，即opers次数的时间。符合题目要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public int[] diffAlgo(int[] nums, int[][] opers) {
    int[] diffArr = new int[nums.length + 1];
    // 初始化差分数组（如果原数组为空，就不需要初始化，即都为0）
    for (int i = 0; i < nums.length; i++) {
        if (i == 0) {
            diffArr[i] = nums[i];
        } else {
            diffArr[i] = nums[i] - nums[i-1];
        }
    }
    for (int i = 0; i < opers.length; i++) {
        int left = opers[i][1];
        int right = opers[i][2];
        int p = opers[i][3];
        if (opers[i][0] == 0) {
            // 加上一个数
            diffArr[left] += p;
            diffArr[right + 1] -= p;
        } else {
            // 减去一个数
            diffArr[left] -= p;
            diffArr[right + 1] += p;
        }
    }

    // 前缀和还原, java不支持数组切片，只能拷贝到新数组
    int[] ans = new int[nums.length];
    ans[0] = diffArr[0];
    // 不要多余的最后一个数，或者写成i < nums.length也可以
    for (int i = 1; i < diffArr.length - 1; i++) {
        ans[i] = ans[i - 1] + diffArr[i];
    }
    return ans;
}

题目补充：1109. 航班预订统计 - 力扣（LeetCode）

二维前缀和

二维前缀和，只是在一维前缀和的基础上，将数组扩展到二维数组，来求答案。对于一个n行m列的二维数组，展示形式如下：代码的数组是从0开始的，这里按代码习惯展示了。

(a00a01…a0(m−1)a10a11…a1(m−1)⋮⋮⋱⋮a(n−1)0a(n−1)1…a(n−1)(m−1))\begin{pmatrix} a{_0}{_0} & a{_0}{_1} & \dots & a{_0}{_{(m-1)}} \\ a{_1}{_0} & a{_1}{_1} & \dots & a{_1}{_{(m-1)}} \\ \vdots & \vdots & \ddots & \vdots \\ a{_{(n-1)}}{_0} & a{_{(n-1)}}{_1} & \dots & a{_{(n-1)}}{_{(m-1)}} \\ \end{pmatrix}

因此，二维前缀和的通项可以表示为：

preSum[n,m]=∑i=0n−1∑j=0m−1aijpreSum[n,m] = \sum_{i=0}^{n-1}\sum_{j=0}^{m-1}a_{ij}

preSum[n,m]表示nums中，nums[0, 0]到nums[n - 1,m - 1]所在的矩阵的和。在前缀和数组上，个人习惯添加前置0，所以对应都需要加1，因此可以创建前缀和数组preSumArr = new long[n + 1][m + 1]（用long避免溢出）。

二维前缀和图，红色区间是到(0,0)的，橘色区间同理。只是颜色被黄色覆盖，未画出

对于原数组nums下标（x, y）处的前缀和：preSumArr[x+1][y+1]=preSumArr[x+1][y]+preSumArr[x][y+1]−preSumArr[x][y]+nums[x][y]preSumArr[x + 1][y + 1] = preSumArr[x + 1][y] + preSumArr[x][y+1] - preSumArr[x][y] + nums[x][y]。
如图所示，由于我们程序计算的先后顺序，我们计算前缀和preSumArr[x2][y2]的时候，已经计算了其正左方(x2, y2-1)、正上方（x2-1, y2）前缀和，由上图可知，（x2, y2）到（0，0）的矩形所在的前缀和，可由(x2, y2 -1) +（x2-1, y2） - (x2 - 1, y2 - 1) 所在区间的和+nums[x2][y2]（即红色区间+橘色区间-黄色区间+nums[x2][y2]）。

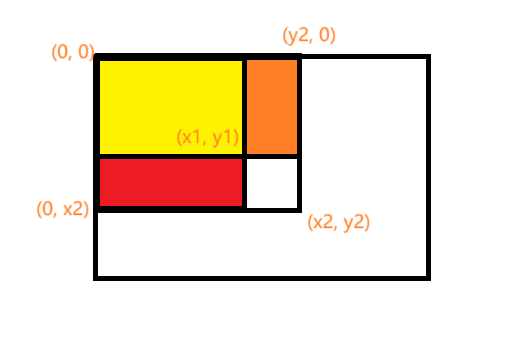
对于nums下标（x1, y1）到（x2，y2）的区间和：
ans=preSumArr[x2+1][y2+1]−preSumArr[x2+1][y1]−preSumArr[x1][y2+1]+preSumArr[x1][y1]ans = preSumArr[x2 + 1][y2 + 1] - preSumArr[x2 + 1][y1] - preSumArr[x1][y2 + 1] + preSumArr[x1][y1]。
如图所示，白色区域的区间和=白色（到(0,0)的）前缀和 - 红色前缀和 - 橘色前缀和 + 黄色前缀和。由于（x1, y1)要被加入到区间和结果，因此白色区域的区间和 = （x2, y2）- (x2, y1 - 1) - (x1 - 1, y2) + (x1 - 1, y1 - 1)

模板题：

【模板】二维前缀和_牛客网 (nowcoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        PrintWriter pw = new PrintWriter(new BufferedOutputStream(System.out));
        // 注意 hasNext 和 hasNextLine 的区别
        int n = sc.nextInt();
        int m = sc.nextInt();
        int q = sc.nextInt();


        // 前缀和数组，加入前置0
        long[][] preSumArr = new long[n + 1][m + 1];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                // 记录输入的数字 并 同时计算前缀和
                preSumArr[i+1][j+1] = sc.nextInt() + preSumArr[i][j + 1] + preSumArr[i + 1][j] - preSumArr[i][j];
            }
        }
        
        for (int i = 0; i < q; i++) {
            // 题目下标从1开始（强烈谴责题目），所以提前减去1还原
            int x1 = sc.nextInt() - 1;
            int y1 = sc.nextInt() - 1;
            int x2 = sc.nextInt() - 1;
            int y2 = sc.nextInt() - 1;
            // 因为加了前置0，所以下面有加1
            long ans = preSumArr[x2 + 1][y2 + 1] - preSumArr[x2 + 1][y1] - preSumArr[x1][y2 + 1] + preSumArr[x1][y1];
            pw.println(ans);
        }
        pw.flush();
    }

}

二维差分

二维差分，同一维差分，在对数组进行区间操作后，最后求区间的值，或打印操作后的数组。

模板题

【模板】二维差分 牛客网 (nowcoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        PrintWriter pw = new PrintWriter(new BufferedOutputStream(System.out));
        // 注意 hasNext 和 hasNextLine 的区别
        int n = sc.nextInt();
        int m = sc.nextInt();
        int q = sc.nextInt();

        long[][] rawArr = new long[n + 2][m + 2];
        long[][] diffArr = new long[n + 2][m + 2];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                rawArr[i][j] = sc.nextInt();
            }
        }
        // 初始化差分数组
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                // 差分公式 diff[i][j] = arr[i][j] - arr[i-1][j] - rawArr[i][j-1] + raw[i-1][j-1]
                diffArr[i][j] = rawArr[i][j] - rawArr[i -1][j] - rawArr[i][j-1] + rawArr[i-1][j-1];
            }
        }

        for (int i = 0; i < q; i++) {
            // 题目下标从1开始
            int x1 = sc.nextInt() - 1;
            int y1 = sc.nextInt() - 1;
            int x2 = sc.nextInt() - 1;
            int y2 = sc.nextInt() - 1;
            int k = sc.nextInt();

            diffArr[x1 + 1][y1 + 1] += k;
            diffArr[x2 + 2][y1 + 1] -=k;
            diffArr[x1 + 1][y2 + 2] -= k;
            diffArr[x2 + 2][y2 + 2] +=k;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                // 差分还原公式
                diffArr[i][j] = diffArr[i][j] + diffArr[i - 1][j] + diffArr[i][j-1] - diffArr[i-1][j-1];
                pw.print(diffArr[i][j] + " ");
            }
            pw.println();
        }
        pw.flush();
    }

}
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可