Songbirds


春

最短路

  • ~18.12K 字
  1. 1. floyd算法
  2. 2. Bellman-Ford算法
  3. 3. SPFA算法
  4. 4. Djkstra算法

图论的最短路问题，介绍可参考百科：最短路问题_百度百科

最短路，部分算法可以解决负权边的问题。但是对于负环（环的和为负数）是无解的，假设在无穷远处有一个负环，他会不顾距离，走到负环处，然后一遍又一遍的走这个负环，直到累计到负无穷，并一直走下去，所以无解。后续如无特殊说明，所有图皆无负环。备注：特殊标明判断负环除外。

有向图，无向图、包括图定义等基础概念不是本篇讨论的问题，因此略去。

对于加权图，我们记为G=(V,E,W)，其中G表示图，V表示点集，E表示边集，W表示加权距离集。后续会用到邻接矩阵图（非本篇所讲基础内容，略），邻接表同理。

在邻接矩阵G表示的图中。对于两点u和v距离，如果u和v为同一点，我们记为G[u][u] = 0，即忽略自环，只取最小值0。若为不同点，则记为G[u][v] = x，为u到达v的最小加权距离。若两点之间无法到达，则记为G[u][v] = +∞+\infty。

floyd算法

关键词

多源、可有负边，时间：O(N^3)，空间：O(N^2)

floyd算法用来求有向图、无向图且可以有负边的多源（以不同点为起点到不同点为终点）最短路。对于无向图，只需要把边拆成两条有向边即可。约定忽略图的自环，自环只会增加长度且无贡献。

题目：有n个编号从1到n点组成m条边的图，求图中的多源最短路。

考虑dp方法。dp[k][i][j] 表示考虑从0到k作为中转节点所有情况，对于dp[k][i][j] 所得到的最小值。即为分别考虑0到k为中转点，i到k到j获得的最小值。

  1. 显然有dp[0][i][j] = G[i][j]成立。即不经过任何点（编号为0的点不存在），最短距离为i于j的初始化距离。
  2. 考虑经过0到k-1作为中转节点的i和j，此时最短路为dp[k-1][i][j]。（考虑了0，即不经过节点中转的情况）
  3. 对于经过0到k节点。由于dp[k-1][i][j]表示考虑0到k-1任一节点中转的最小距离。即目前i到j的最小距离已经知道为dp[k-1][i][j]，此时考虑增加k节点中转，于是最短距离变为，原本经过k-1的最短距离 或 i到k的最短距离 加上 k 到 j 的最短距离中的最小值。
    即在原有的0到k-1的i与j最小值路径上插入k节点，因为如3点开头所说我们只需要考虑经过0到k的节点。

由此可以推断出考虑0到k中转的i和j的最短路为dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])

即：若插入k节点，会使距离变小，则更新这个距离

因此递推公式为：

dp[k][i][j]=min(dp[k−1][i][j],dp[k−1][i][k]+dp[k−1][k][j])dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])

因此有伪代码：

其中k是转移阶段，当我们求k中转的时候，k-1与之前的所有数组值必须已经求出。

1
2
3
4
for k := 1 to n:
  for u := 1 to n:
    for v := 1 to n:
      f(k,u,v) := min{f(k-1,u,v), f(k-1,u,k)+f(k-1,k,v)}

我们注意到，取k中转的时候，只与k-1数组的值相关，因此，可以考虑滚动数组优化空间。
更进一步的，我们可以直接复用u、v的数组，（证明暂缺😁，不会就是不会）。

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]) 

1
2
3
4
for k := 1 to n:
  for u := 1 to n:
    for v := 1 to n:
      f(u,v) := min{f(u,v), f(u,k)+f(k,v)}

因此时间复杂度为O(N^3)，空间复杂度为O(N^2)。

完整代码：

注意：此代码是基于节点编号从1到n，如果从0到n-1，初始化图的代码不使用n+1。打印也从0开始。基于无向图。代码中，在遇到无穷大时不中转也很重要，保证了无穷大的一致：if (graphArr[i][k] != inf && graphArr[k][j] != inf)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public static void main(String[] args) {
    int inf = 0x3f3f3f3f;
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    int m = sc.nextInt();
    // 初始化图
    int[][] graphArr = initGraph(inf, sc, n, m);
    // 跑floyd,
    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                // 如果某条中转路径无穷大，则不中转。如果不加此判断，其中一个无穷大加上一个负数边权会变小。
                // 虽然相加值很大，仍然可以表示无穷，但是多个无穷数会不一样。很重要。
                if (graphArr[i][k] != inf && graphArr[k][j] != inf) {
                    graphArr[i][j] = Math.min(graphArr[i][j], graphArr[i][k] + graphArr[k][j]);
                }
            }
        }
    }
    // 输出答案
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            System.out.print(graphArr[i][j]);
            System.out.print(" ");
        }
        System.out.println();
    }
}

private static int[][] initGraph(int inf, Scanner sc, int n, int m) {
    int[][] graphArr = new int[n + 1][n + 1];
    // 初始化图，根据题目节点编号从1开始
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i != j) {
                graphArr[i][j] = inf;
            }
        }
    }
    // 设置图的初始距离
    for (int i = 0; i < m; i++) {
        int u = sc.nextInt();
        int v = sc.nextInt();
        int w = sc.nextInt();
        // 因为是无向图
        graphArr[u][v] = w;
        graphArr[v][u] = w;
    }
    
    return graphArr;
}

记录路径核心代码：基于有向图，原因见图初始化注释。代码中保证了无穷大一致，后面才可以直接用inf判断无穷大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
public static void main(String[] args) {
    int inf = 0x3f3f3f3f;
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt(); // n 个节点
    int m = sc.nextInt(); // 接下来m行表示边的关系
    // 初始化图（同上、略）
    int[][] graphArr = initGraph(inf, sc, n, m);
    // path数组，path[i][j] 的值表示 更新从i到j的最短路径时，经过的一个中转点
    int[][] path = new int[n + 1][n + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            // 初始化i到j的最优解时i直接到j
            path[i][j] = j;
        }
    }
    // 跑floyd,
    for (int k = 1; k <= n; k++) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                // 如果某条中转路径无穷大，则不中转。如果不加此判断，其中一个无穷大加上一个负数边权会变小。
                // 虽然相加值很大，仍然可以表示无穷，但是多个无穷数会不一样。很重要。
                if (graphArr[i][k] != inf && graphArr[k][j] != inf) {
                    // 这里要改一下，不能简写min，只有能够更小的时候才更新path
                    if (graphArr[i][k] + graphArr[k][j] < graphArr[i][j]) {
                        graphArr[i][j] = graphArr[i][k] + graphArr[k][j];
                        // 此时的i--->j的最优解不再是j了而是 i--->k----
                        path[i][j] = path[i][k];
                    } else if (graphArr[i][k] + graphArr[k][j] == graphArr[i][j]) {
                        // 如果相同，取字典序小的，同时如果k=i或j，则不更新，避免陷入自己到自己移动方式。
                        // （例如本来是2到3，代码里经过2中转距离与2到3的距离相等，会陷入2到2的问题）
                        if (k != i && k != j && path[i][k] < path[i][j]) {
                            path[i][j] = path[i][k];
                        }
                    }
                }
            }
        }
    }
    // 输出路径
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            System.out.print(i + "-->" + j + ": ");
            System.out.print(i);
            int s = i;
            while (s != j) {
                System.out.print("-->" + path[s][j]);
                s = path[s][j];
            }
            System.out.print(" ");
            // 因为确保了无穷大一样为inf，所以这里可以直接判断inf
            if (graphArr[i][j] == inf) {
                System.out.println("  路径不存在");
            } else {
                System.out.println("  road cost: " + graphArr[i][j]);
            }
        }
    }
}

private static iht[][] initGraph(int inf, Scanner sc, int n, int m) {
    int[][] graphArr = new int[n + 1][n + 1];
    // 初始化图为正无穷，根据题目节点编号从1开始
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i != j) {
                graphArr[i][j] = inf;
            }
        }
    }
    // 设置图的初始距离
    for (int i = 0; i < m; i++) {
        int u = sc.nextInt();
        int v = sc.nextInt();
        int w = sc.nextInt();
        // 无向图跑不了负数边（假设a到b点，边权为负数，则会a到b，再b到a，无限重复到负无穷）。
        // 所以为了体现floyd可以跑负数边的特性，这里用有向图演示
        graphArr[u][v] = w;
        // graphArr[v][u] = w;
    }
    
    return graphArr;
}

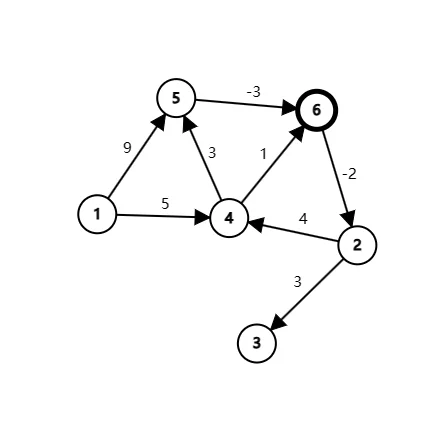
一组测试用例，包含负数边，所以是有向图。
第一行包含两个数n、m。n表示有编号从1到n的n个节点，m表示接下来m行。
接下来m行，每行三个整数 u，v，w，代表 u到v（单向）存在一条边权为w的边。

1
2
3
4
5
6
7
8
9
6 8
6 2 -2
4 6 1
5 6 -3
1 4 5
1 5 9
2 3 3
2 4 4
4 5 3

floyd测试用例

Bellman-Ford算法

关键词

单源、可有负边，可判断负环，时间：O(mn)，空间：O(N)。

BF算法基于松弛操作。

松弛操作：对于起点S的图，存在边(u,v)，dis(v) = min(dis(v), dis(u) + w(u, v))。即如果经过u能够使起点到v的距离变小，则更新为这个小的距离。其中dis(v)表示当前起点到v的最小距离。

BF算法的思想主要是对所有边进行松弛操作，直到松弛操作无变化为止，此时说明已找起点s到其他点最短路。最多需要对每条边松弛n-1次操作即可，在一个n个顶点的图中，任意两点之间的最短路径最多有n-1个边（如果更多，则说明有冲边或者环），在经过一轮松弛后，得到是源点经过一条边到达其他点的距离，经过k轮松弛后，是源点经过k条边到其他顶点的距离。如果第n次松弛操作仍然值有改变，则说明有负环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
private final static int inf = 0x3f3f3f3f;

//用于存放起点s到其它顶点之间的最短距离，下标0处的点不使用
public static long[] dis;

public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    int m = sc.nextInt();
    // 在确定边数的情况下可以用数组，如果是双向与单向混用则需要使用list存储
    ArrayList<Edge> edges = new ArrayList<>();
    for (int i = 0; i < m; i++) {
        int u = sc.nextInt();
        int v = sc.nextInt();
        int w = sc.nextInt();
        edges.add(new Edge(u, v, w));
    }
    if (bellmanford(n, edges, 1)) {
        // 无负环
        System.out.println("NO");
    } else {
        System.out.println("YES");
    }
}

public static boolean bellmanford(int n, List<Edge> edges, int s) {
    dis = new long[n + 1];
    for (int i = 1; i <= n; i++) {
        //初始化第1个顶点到其它n个顶点之间的距离为无穷大
        dis[i] = inf;
    }
    // 起点到起点的距离为0
    dis[s] = 0;
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < edges.size(); j++) {
            Edge edge = edges.get(j);
            // 保证点是可以到达的，从dis[s] = 0开始出发
            if (dis[edge.u] == inf) {
                continue;
            }
            // 起点到V到距离 = min(起点到v的距离，起到到u的距离+ u到v的边权w)
            // 释义：起点到v的距离，如果能够经过边u-v松弛变小，则松弛
            dis[edge.v] = Math.min(dis[edge.v], dis[edge.u] + edge.w);
        }
    }
    // 第n次操作，判断是否松弛，若松弛，则说明有负环
    boolean judge = true;
    for (int j = 0; j < edges.size(); j++) {
        Edge edge = edges.get(j);
        if (dis[edge.u] == inf || dis[edge.v] == inf) {
            continue;
        }
        if (dis[edge.v] > dis[edge.u] + edge.w) {
            judge = false;
            break;
        }
    }
    return judge;
}

//内部类，表示图的一条加权边
static class Edge {
    public int u;   //边的起点
    public int v;   //边的终点
    public int w;  //边的权值

    Edge(int u, int v, int w) {
        this.u = u;
        this.v = v;
        this.w = w;
    }
}

一点优化：在不需要判断是否有负环的情况下，for (int i = 1; i < n; i++) 第一个for循环改为while循环，同时判断是否有松弛，若无松弛，则此刻已经找到最短路，停止后续遍历。

SPFA算法

关于SPFA，他死了😂。（玩笑）。SPFA，即队列优化版Bellman-Ford算法，拥有BF算法的一切特性。其平均时间复杂度为O(km)，k为每个节点平均入队次数。k大概为4左右。但是其最坏时间复杂度为O(mn)，目前对于堆优化版Dijkstra能过得题基本上都会卡SPFA。
所以，对于单源最短路，若无负权边，用堆优化版Dijkstra。若有负权边，且没有特殊性质，若SPFA能过，则BF算法一定能过（主要是BF比SPFA好写。当然平均SPFA比BF还是快的）。
对于多源最短路。若有负权变，如果数据范围允许，考虑floyd，若不允许，则应当考虑johnson算法。若无负权边，跑n遍单源最短路，或者直接多源最短路，选出一个能过时间复杂度的数据即可。

建图方式为了节省内存使用了链式前向星。链式前向星可以参考深度理解链式前向星_dijskra_ACdreamers的博客-CSDN博客。(ps：现在一般不会使用链式前向星了，大多都是邻接表，使用List<List>建图。由于List的容量会存在浪费的可能，为了节省内存，也可以使用List[]，数组大写为n，表示n个List组成的数组)。
(不知道是否时语言原因，java还是MLE了🤣🤣。C++的好处就是大多数评测样例都是按C++来算时间与内存的)。

链式前向星写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
public class Spfa {

    // 根据题目意思不同，需要输出不同的无穷大，此处输出0
    private static final int INF = 0x3f3f3f3f;

    private static long[] dis;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int s = sc.nextInt();

        dis = new long[n + 1];

        // 边集，因为点从1开始，所以边也从1开始
        Edge[] edges = new Edge[m + 1];
        for (int i = 1; i < m + 1; i++) {
            edges[i] = new Edge(0, 0, 0);
        }
        // 点集
        int[] head = new int[m + 1];
        int numEdge = 0;
        for (int i = 0; i < m; i++) {
            // 起点
            int from = sc.nextInt();
            // 终点
            int to = sc.nextInt();
            // 边权
            int wei = sc.nextInt();
            // 建图
            // 当前边的编号。从1开始，因为点从1开始
            numEdge++;
            // 当前读入的这条边的上一条边
            edges[numEdge].next = head[from];
            // 更新当前边的终点
            edges[numEdge].to = to;
            // 更新当前边的长度
            edges[numEdge].wei = wei;
            // 到当前读入的边为止（不包括这条边） 的上一条边的序号；
            head[from] = numEdge;
        }

        spfa(edges, head, n, s);
        for (int i = 1; i <= n; i++) {
            if (s == i) {
                System.out.print("0" + " ");
            } else {
                System.out.print(dis[i] + " ");
            }
        }
    }

    private static void spfa(Edge[] edges, int[] head, int n, int s) {
        ArrayDeque<Integer> queue = new ArrayDeque<>();
        // 是否存入队列中
        boolean[] vis = new boolean[n + 1];
        for (int i = 1; i <= n; i++) {
            dis[i] = INF;
            vis[i] = false;
        }
        // 将起点存入队列，并将距离记为0，标记已经入队
        queue.add(s);
        dis[s] = 0;
        vis[s] = true;

        while (!queue.isEmpty()) {
            // 弹出、并标记已经出队
            int u = queue.pollFirst();
            vis[u] = false;
            // （链式前向星遍历邻接表）扫描所有出边
            for (int i = head[u]; i >= 1; i = edges[i].next) {

                int v = edges[i].to;
                // 如果有最短路就更改
                if (dis[v] > dis[u] + edges[i].wei) {
                    dis[v] = dis[u] + edges[i].wei;
                    // 未入队则入队
                    if (!vis[v]) {
                        // 标记入队
                        vis[v] = true;
                        queue.addLast(v);
                    }
                }
            }
        }
    }

    static class Edge {
        // 当前边的上一个边
        public int next;
        // 当前边的终点
        public int to;
        // 当前边的长度
        public int wei;

        public Edge(int next, int to, int wei) {
            this.next = next;
            this.to = to;
            this.wei = wei;
        }
    }
}

Djkstra算法

关键词

单源、只可有正边，时间：O(n^2)，空间：O(N)。适合于稠密图。

堆优化版，O(mlogm)，空间：O(m+n)。适合于稀疏图。

注意，如果图为稠密图，堆优版不一定优于暴力版。

朴素dijkstra算法

dijkstra是基于贪心思想的最短路算法，该算法将点分为已经访问过的点和未访问过的点（代码用vis数组区分），已经访问的点都是起点到该点最短距离已经确定的点。每一次从未访问的点中选择距离起点最近的点，作为下一个访问的点，标记为已访问，同时使用该点更新其他点距离（主要是更新相邻点的距离，由于不确定哪些点，简单的做法就是尝试更新所有点）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
public class Dijkstra {

    private final static int inf = 0x3f3f3f3f;

    private static long[] dis;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); // n 个节点
        int m = sc.nextInt(); // 接下来m行表示边的关系
        int s = sc.nextInt(); // 起点

        // 初始化图
        int[][] graphArr = initGraph(sc, n, m);

        dijkstra(n, s, graphArr);

        for (int i = 1; i <= n; i++) {
            if (s == i) {
                System.out.print("0" + " ");
            } else {
                System.out.print(dis[i] + " ");
            }
        }
    }

    private static void dijkstra(int n, int s, int[][] graphArr) {
        // 是否访问数组
        boolean[] vis = new boolean[n + 1];
        // 初始化起点到其他点的距离为无穷大
        // 存储起点到其他点的最短距离
        dis = new long[n + 1];
        Arrays.fill(dis, inf);
        dis[s] = 0;

        // 为什么此刻不能将其标记为True？
        // 代码写法原因，如果此刻标记为true，那么!vis[s],就为false,第一次进入时由于u == -1，可能将u更新为点1或点2为最短（非起点序号最小的点），
        // 除了起点外，其他点距离都是无穷大，dis[j] < dis[u]永远为false，显然这是错误的，离起点最短距离点是与编号无关的。
        // vis[s] = true;

        for (int i = 1; i <= n; i++) {
            // u表示未访问的点中，距离起点最短的点
            // 初始化u = -1，用来先在未访问的点中挑一个点
            int u = -1;
            for (int j = 1; j <= n; j++) {
                if (!vis[j] && (u == -1 || dis[j] < dis[u])) {
                    // 设置u为距离起点最短的点
                    u = j;
                }
            }
            // 标记u已经访问
            vis[u] = true;
            for (int v = 1; v <= n; v++) {
                // 通过点u更新其他点的距离（主要是更新u点的相邻距离，因为dis[u]既然为当前最小，那么其一定有值，不是无穷大）
                // dis[u] + graphArr[u][v] 则能更新起点到v的距离
                dis[v] = Math.min(dis[v], dis[u] + graphArr[u][v]);
            }
        }
    }

    private static int[][] initGraph(Scanner sc, int n, int m) {
        int[][] graphArr = new int[n + 1][n + 1];
        // 初始化图，根据题目节点编号从1开始
        for (int i = 1; i <= n; i++) {
            Arrays.fill(graphArr[i], inf);
            graphArr[i][i] = 0;
        }
        // 设置图的初始距离
        for (int i = 0; i < m; i++) {
            int u = sc.nextInt();
            int v = sc.nextInt();
            int w = sc.nextInt();
            graphArr[u][v] = Math.min(graphArr[u][v], w);
        }

        return graphArr;
    }

}

堆优化版dijkstra算法

在寻找未访问过的点i（vis[i]=false），且离起点最近的点时，我们可以采用堆优化，从而将时间复杂度降低到mlogn。备注：时间复杂度mlogm，建议用于稀疏图，稠密图可以理解为图中m=n^2。
复杂度分析：大部分在注释中已经分析，每条边最多入优先队列一次，最多入队列m条边，因此时间复杂度为O(mlogm)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
private final static int inf = 0x3f3f3f3f;

private static void dijkstraWithHeap(int n, int s, int[][] edges) {
    // dijkstra堆优版一般用于稀疏图，所以特殊用邻接表,因为要存权重值，所以里面的值用int[]数组存储，
    // int[]共两位，0位表示终点v，1位表示权重w
    List<int[]>[] graphArr = new List[n + 1];
    for (int i = 0; i < graphArr.length; i++) {
        graphArr[i] = new ArrayList<>();
    }
    // 建图
    for (int[] edge : edges) {
        int u = edge[0];
        int v = edge[1];
        int w = edge[2];
        graphArr[u].add(new int[]{v, w});
    }

    int[] dis = new int[n + 1];

    // 是否访问数组
    boolean[] vis = new boolean[n + 1];
    // 初始化起点到其他点的距离为无穷大
    // 存储起点到其他点的最短距离
    dis = new int[n + 1];
    Arrays.fill(dis, inf);
    dis[s] = 0;

    // 优先队列，按距离起点的距离升序排序

    PriorityQueue<int[]> queue = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
    queue.add(new int[]{s, 0});
    while (!queue.isEmpty()) {
        int[] node = queue.poll();
        // 当前未访问的点中距离起点最近的点u
        int u = node[0];
        // u被访问过，不继续访问u
        if (vis[u]) {
            continue;
        }
        vis[u] = true;
        // 遍历u连通的点，每条边最多会遍历一次（如上u已经被访问，则不会继续遍历与u相连的边），总共最多遍历m次
        for (int[] graph : graphArr[u]) {
            int v = graph[0];
            int w = graph[1];
            // 如果起点到v能够被u松弛，则松弛，同时v入堆，会有点重复入堆，但是入堆最多m次，因为for遍历最多m次
            // 对于重复入堆的点，第1次访问后，我们标记vis[i]为true，不再访问。
            if (dis[u] + w < dis[v]) {
                dis[v] = dis[u] + w;
                queue.add(new int[]{v, dis[v]});
            }
        }
    }
}
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可