《数据结构与算法分析Java语言描述》第六章6.1节读书笔记
优先队列又称为堆,是用来处理具有优先级的元素的数据结构。
6.1 模型
优先队列分为两种。
一种是小顶堆实现的优先队列,在堆顶是最小的元素,每次可以直接访问最小的元素。
另一种是大顶堆实现的优先队列,在堆顶是最大元素。每次可以直接访问最大的元素。
对于小顶堆而言,至少支持两种操作,insert插入,将元素按优先级插入到指定位置,deletemin删除,删除堆顶的最小元素。insert操作等价于入队,deletemin等价于出队。(由堆的优先级,可以引出堆排序)。
后续以小顶堆为例。
6.2 一些简单实现
使用有序链表来实现,表头的元素最小,则每次deleteMin的时间复杂度是O(1),对于N个元素,则是O(N)。对于每次insert操作,由于需要遍历找到插入的位置,时间复杂度是O(N),对于N个元素,则是O(N2)。
使用二叉查找树实现,二叉查找树两种操作实现皆是O(logN),对于N个元素,实现是O(NlogN)。不过二叉查找树的实现较为复杂,而且许多支持的操作我们并不需要。将实现二叉堆,来支持这个操作,并且时间复杂度都是O(NlogN)。
6.3 二叉堆
堆一般指二叉堆。堆具有结构性和堆序性。对堆的一次操作,可能会破坏这两个性质中的一个。因此对于堆一次操作,必须还原这两个性质,才算作一次操作终止。
6.3.1 结构性质
堆是一棵完全二叉树,除最底层外,每一层都被填满。容易证明一棵高为h的完全二叉树有2h到2h+1−1个节点。即节点个数N=2h或2h+1−1个节点,因此,高度h=O(logN)。
堆性质:堆大多都由数组实现,而不是链表。对于数组上的任一位置i的元素,其左儿子在2i,右儿子在2i+1。它的父亲在i/2上(java的整除的性质,对于节点i,无论他是左儿子,还是右儿子,整除得到的结果都是i/2)。
由于是用数组实现,当我们遍历所有元素时,可以直接通过计算,来得知访问的下标。例如下标1的左儿子在下标2,右儿子在下标3。按顺序访问。
**本节我们图示皆以二叉树展示,但是实现仍然是数组。**实现的是小顶堆。
注意:我们的堆数组,下标为0的位置是不使用的,因为2i = 0,得到的结果和父节点是一样的位置。所以有效节点从1开始。(线段树也是如此,使用数组实现树,且0的位置不使用)。
6.3.2 堆序性
对于小顶堆,根节点应该是最小的元素。同时,对于二叉堆的任意子树,也是一个小顶堆,子树的根节点也应该是子树的最小元素。
因此,对于一个小顶堆,对于任意节点i,如果其有左右子节点,则应该满足,num[i] <= num[2i],num[i] <= num[2i + 1]。
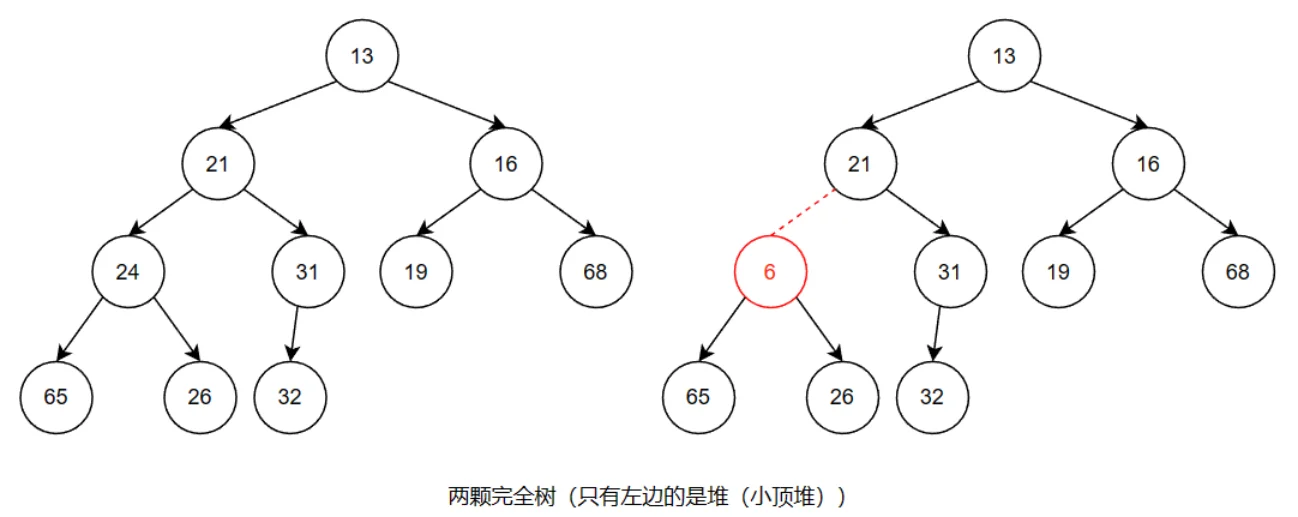
根据堆序性,最小的元素总是可以以O(1)的时间在堆的根处找到。实现为findMin。
6.3.3 堆的基本操作
插入(insert)
为了将一个元素X插入到堆中,可以先在下一个可用的位置创建一个空节点。如果X可以放入该节点而不破化堆序性,那么插入完成。否则空节点应该朝着根的方向冒一步。继续该过程,知道X能被放入空节点为止。如下图,为了插入14,先创建空节点,插入14不满足,将空节点上冒,知道将14插入正确的位置。
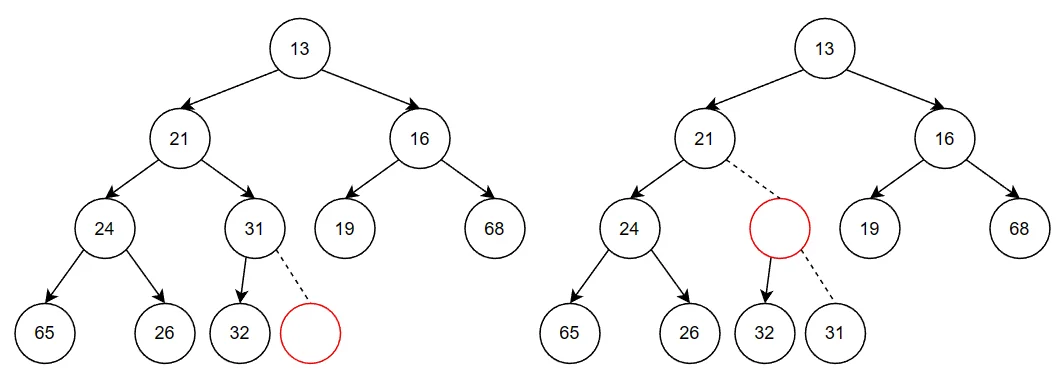
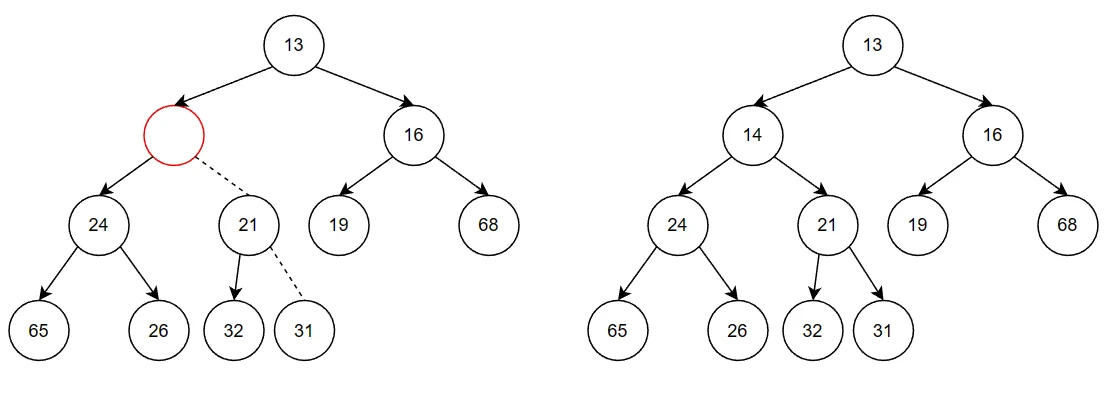
这种策略一般叫做上滤,新元素在堆中上滤知道找出正确的位置。使用如下代码实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public void insert(T x) {
if (currentSize == array.length - 1) {
this.enlargeArray(array.length * 2 + 1);
}
currentSize++;
int hole = currentSize;
for (array[0] = x; x.compareTo(array[hole / 2]) < 0; hole /= 2) {
array[hole] = array[hole / 2];
}
array[hole] = x;
}
|
如果要插入的元素是最小的元素,那么他将一直被推向顶端。
deleteMin(删除最小元素)
最小的元素在顶端,即下标为1处。删除最小的元素,要在根节点(下标1处)建立一个空穴。将空穴中的两个字节的的较小值移入空穴,则空穴下移动一层。重复这一过程。最后再将堆中的最大元素(如图31)被移入空穴。
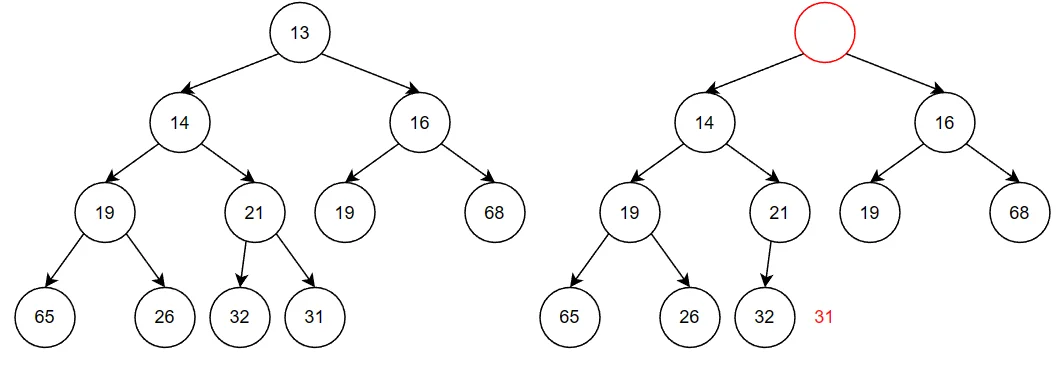
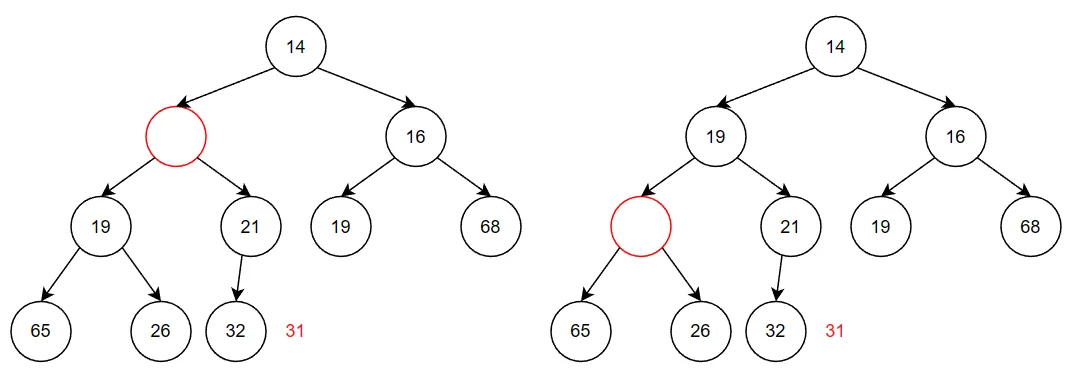
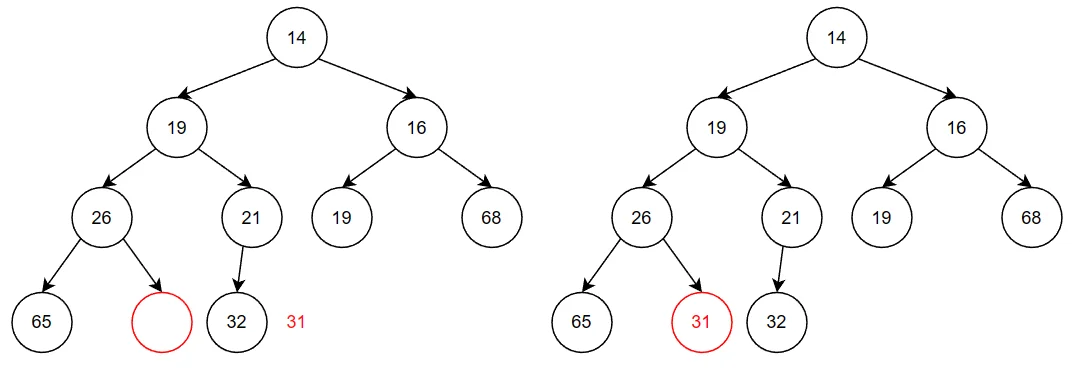
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| public T deleteMin() {
if (currentSize == 0) {
throw new RuntimeException();
}
T minItem = array[1];
array[1] = array[currentSize];
currentSize -= 1;
percolateDown(1);
return minItem;
}
private void percolateDown(int hole) {
int child;
T temp = array[hole];
for (; hole * 2 <= currentSize; hole = child) {
child = hole * 2;
if (child != currentSize && array[child + 1].compareTo(array[child]) < 0) {
child++;
}
if (array[child].compareTo(temp) < 0) {
array[hole] = array[child];
} else {
break;
}
}
array[hole] = temp;
}
|
建堆
通过初始构造集合建堆,可以考虑建堆使用N个insert方法来建堆,每个insert的平均时间是O(1),而最坏的时间是O(lgN)。因此总的平均时间为O(N),总的最坏时间为O(NlgN)。
一般的算法是将N项以任意顺序放入堆中,保持结构性,此时percolateDown(i)从节点i下滤,使用如下的程序创建一棵堆序的树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public BinaryHeap(T[ ] items ) {
currentSize = items.length;
array = (T[]) new Comparable[ ( currentSize + 2 ) * 11 / 10 ];
int i = 1;
for(T item : items ) {
array[i++] = item;
}
buildHeap();
}
private void buildHeap() {
for (int i = currentSize / 2; i > 0; i--) {
percolateDown(i);
}
}
|
6.4 完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
| public class BinaryHeap<T extends Comparable<? super T>> {
private static final int DEFAULT_CAPACITY = 10;
private int currentSize;
private T[] array;
public BinaryHeap() {
this(DEFAULT_CAPACITY);
}
public BinaryHeap(int capacity) {
currentSize = 0;
array = (T[]) new Comparable[capacity + 1];
}
public BinaryHeap(T[] items) {
currentSize = items.length;
array = (T[]) new Comparable[(currentSize + 2) * 11 / 10];
int i = 1;
for (T item : items) {
array[i++] = item;
}
buildHeap();
}
private void buildHeap() {
for (int i = currentSize / 2; i > 0; i--) {
percolateDown(i);
}
}
public void insert(T x) {
if (currentSize == array.length - 1) {
this.enlargeArray(array.length * 2 + 1);
}
currentSize++;
int hole = currentSize;
for (array[0] = x; x.compareTo(array[hole / 2]) < 0; hole /= 2) {
array[hole] = array[hole / 2];
}
array[hole] = x;
}
public T deleteMin() {
if (currentSize == 0) {
throw new RuntimeException();
}
T minItem = findMin();
array[1] = array[currentSize];
currentSize -= 1;
percolateDown(1);
return minItem;
}
public T findMin() {
if (isEmpty()) {
throw new RuntimeException();
}
return array[1];
}
public boolean isEmpty() {
return currentSize == 0;
}
private void percolateDown(int hole) {
int child;
T temp = array[hole];
for (; hole * 2 <= currentSize; hole = child) {
child = hole * 2;
if (child != currentSize && array[child + 1].compareTo(array[child]) < 0) {
child++;
}
if (array[child].compareTo(temp) < 0) {
array[hole] = array[child];
} else {
break;
}
}
array[hole] = temp;
}
private void enlargeArray(int newSize) {
T[] old = array;
array = (T[]) new Comparable[newSize];
for (int i = 0; i < old.length; i++) {
array[i] = old[i];
}
}
public static void main(String[] args) {
int numItems = 10000;
BinaryHeap<Integer> h = new BinaryHeap<>();
int i = 37;
for (i = 37; i != 0; i = (i + 37) % numItems) {
h.insert(i);
}
for (i = 1; i < numItems; i++) {
System.out.println(h.findMin());
h.deleteMin();
}
}
}
|





