《数据结构与算法分析Java语言描述》第五章5.4节读书笔记
分离链接法的缺点是使用了散列表,给这些新单元分配地址需要时间,导致算法速度有些减慢。另一种不使用链表的解决方法是尝试另外一些单元,直到找出单元为止。常见的是单元h0(x),h1(x),h2(x),...相继被试选,其中hi(x)=(hash(x)+f(i))modTableSize,且f(0) = 0。函数f是冲突解决方法。一般来说其装填因子λ=0.5。这样的表叫做探测散列表。
5.4.1 线性探测法
线性探测法中,冲突解决函数f是i的线性函数,典型的是f(i) = i (i >= 0, i++)。这相当于冲突时,从冲突的地址+i,i从0递增,直到找到一个空的位置插入。如下是对于一个长度为10的散列表插入[89, 18, 49, 58, 69]时的情况。解决冲突的函数是f(i) = i。
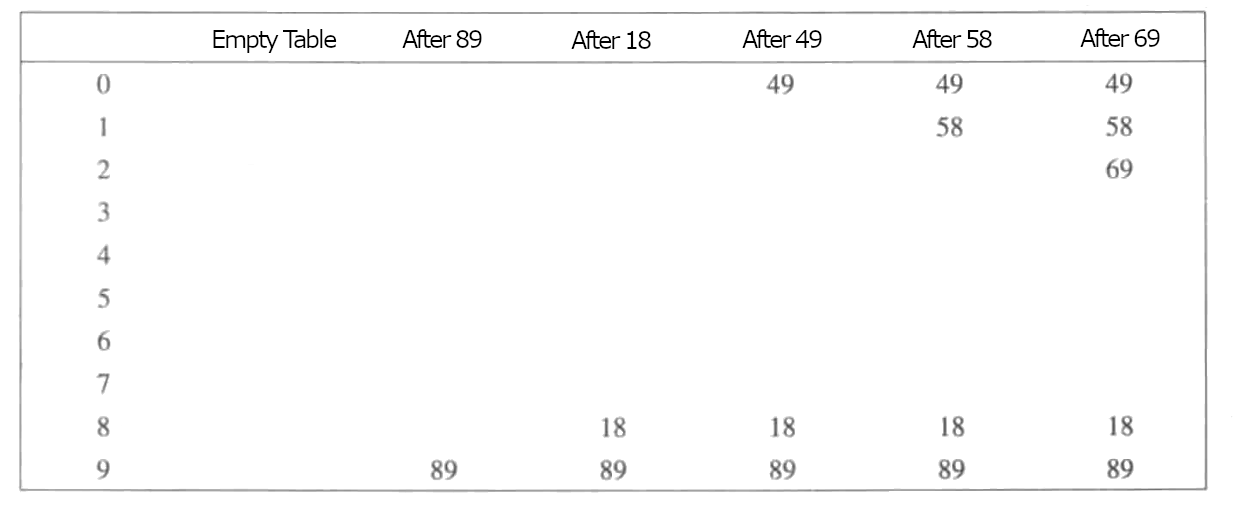
第一次冲突是在插入49时出现冲突(hash(x) = x),根据冲突解决公式,h(49)=(hash(49) + 1) mod 10时。冲突解决,结束,49放入该位置。第二次是插入58时出现冲突,h(58) = (hash(58) + 3) mod 10时。冲突解决。由上可知,每次冲突出现时,只需要沿着冲突的位置继续向下寻找可用位置,直到解决冲突即可。只要表足够大,总可以找到一个空位置。但是可能花费较多的时间。另外,占据的单元会开始形成一些区块,其结果称为一次聚集。当出现冲突后,可能会需要多次试选才能解决冲突。
可以得到证明,(证明较为复杂)。使用线性探测,预期探测次数对于插入和不成功查找约为:21(1+(1−λ)21),而成功的查找来说则是21(1+1−λ1)。则插入与不成功查找的需要相同的次数,成功查找的次数比不成功查找的平均花费时间较少。
如果λ=0.75,则上述公式预计线性一次插入需8.5次探测,如过0.9,则需要50次探测。由此可以看到,如果表有超过一半被装填满的时候,线性探测法不是一个好的方法。
5.4.2 平方探测法
平方探测法是为了解决线性探测法的一次聚集问题。较为流行的选择f(i)=i2,这相当于冲突时,加i2,i从0开始递增,如下图,当49与89冲突时,放入0位置。下次58放入时,则按公式依次选择后,放入2位置。
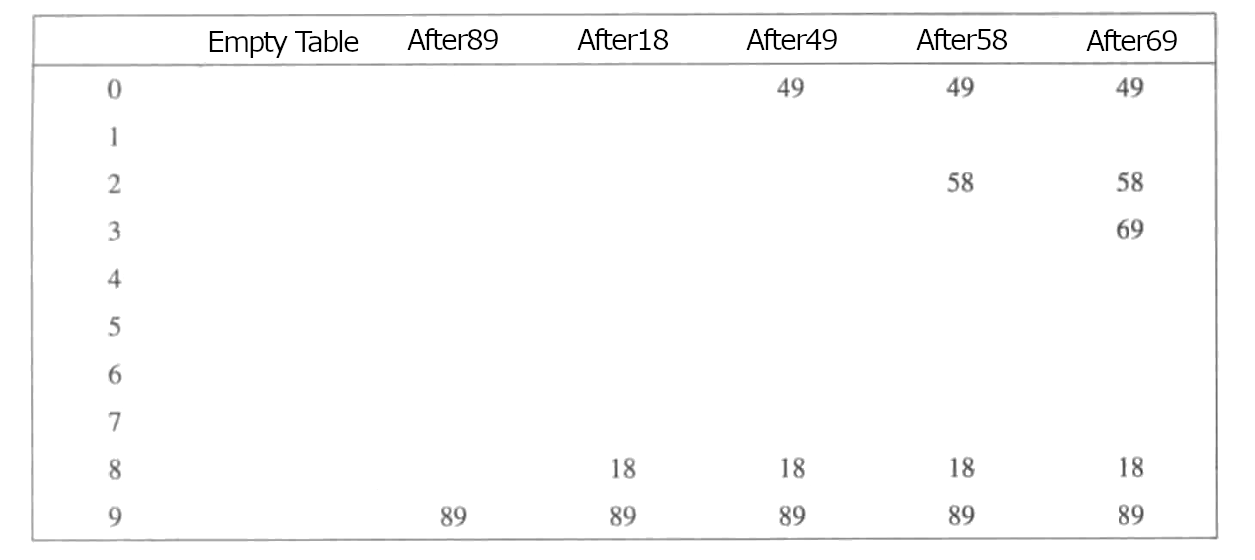
对于平方探测法,一旦表的填充超过一半,则不够好。特别的,如果表的大小不是素数,在被填充一半之前,就不能一次找到空的单元了,证明如下。
定理5.1:如果使用平方探测法,且表的大小是素数,那么当表小于一半的时候,总能够插入一个元素。
证明:采用反证法
令表的大小TableSize是一个大于3的素数,证明前TableSize/2个备选位置是互异的。h(x)+i2(modTableSize)和h(x)+j2(modTableSize)是这些位置的其中两个,其中0 <= , j <= TableSize/2 (注意会向下取整,且tableSize是素数)。为推出矛盾,我们假设前两个位置相同,但i=j,于是有
h(x)+i2=h(x)+j2(modTableSize)
i2=j2(modTableSize)
(i−j)+(i+j)=0(modTableSize)
由于TableSize是素数,要么i - j = 0,要么i+j=0。由于i,j互异,则第一个选择不可能,又因为0 <= i,j <= tableSIze/2,则第二个选择不可能。从而,前tableSize/2个备选位置都是互异的。则推出如上定理5.1。
即使表的填充位置只比一半多一个,则也可能插入失败。同时删除操作不能执行,因为相应的单元可能已经引起冲突,元素绕过它存在了别处,那么所有剩下的contains操作都会失败,因此探测表散列需要惰性删除,
探测表散列的大部分实现如下,此处不使用链表数组,使用单元数组HashEntry,其每一项有下列三种情形:
- null
- 非null,且该项是活动的(isActive 为true)
- 非null,且该项已被标记删除(isActive 为false)
ps: 判断是否时素数isPrime()方法,平方探测findPos()具体后移动平方的实现方法,这两个方法经典。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
| public class QuadraticProbingHashTable<AnyType> {
private static final int DEFAULT_TABLE_SIZE = 11;
private HashEntry<AnyType>[] array;
private int currentSize;
public QuadraticProbingHashTable() {
this(DEFAULT_TABLE_SIZE);
}
public QuadraticProbingHashTable(int size) {
allocateArray(size);
makeEmpty();
}
public void makeEmpty() {
currentSize = 0;
Arrays.fill(array, null);
}
private void allocateArray(int arraySize) {
this.array = new HashEntry[nextPrime(arraySize)];
}
public boolean contains(AnyType x) {
int currentPos = findPos(x);
return isActive(currentPos);
}
public int size() {
return currentSize;
}
public int capacity() {
return array.length;
}
public boolean insert(AnyType x) {
int currentPos = findPos(x);
if (isActive(currentPos)) {
return false;
}
array[currentPos] = new HashEntry<>(x, true);
currentSize++;
if (currentPos > array.length / 2) {
rehash();
}
return true;
}
public boolean remove(AnyType x) {
int currentPos = findPos(x);
if (isActive(currentPos)) {
array[currentPos].isActive = false;
currentSize--;
return true;
} else {
return false;
}
}
private void rehash() {
HashEntry<AnyType>[] oldArray = array;
allocateArray(2 * oldArray.length);
currentSize = 0;
for (HashEntry<AnyType> entry : oldArray) {
if (entry != null && entry.isActive) {
insert(entry.element);
}
}
}
private int findPos(AnyType x) {
int offset = 1;
int currentPos = myHash(x);
while (array[currentPos] != null && !array[currentPos].element.equals(x)) {
currentPos += offset;
offset += 2;
if (currentPos >= array.length) {
currentPos -= array.length;
}
}
return currentPos;
}
private boolean isActive(int currentPos) {
return array[currentPos] != null && array[currentPos].isActive;
}
private int myHash(AnyType x) {
int hashVal = x.hashCode();
hashVal %= array.length;
if (hashVal < 0) {
hashVal += array.length;
}
return hashVal;
}
private static int nextPrime(int arraySize) {
if (arraySize % 2 == 0) {
arraySize++;
}
while (!isPrime(arraySize)) {
arraySize += 2;
}
return arraySize;
}
private static boolean isPrime( int n ) {
if( n == 2 || n == 3 ) {
return true;
}
if( n == 1 || n % 2 == 0 ) {
return false;
}
for( int i = 3; i * i <= n; i += 2 ) {
if( n % i == 0 ) {
return false;
}
}
return true;
}
private static class HashEntry<AnyType> {
public AnyType element;
public boolean isActive;
public HashEntry(AnyType element) {
this.element = element;
}
public HashEntry(AnyType element, boolean isActive) {
this.element = element;
this.isActive = isActive;
}
}
}
|
平方探测法解决了一次聚集,但是散列(计算到插入同一位置)到同一位置时,将继续往后探索相同的备选单元。这称为二次聚集。下面的双散列将解决这个问题,代价是要计算一个附加的散列函数。
5.4.3 双散列
双散列简单来说就是采取两个散列函数,其中一个散列计算具体的落入的位置,第二个散列是在冲突后,要从冲突的位置移动的步长。例如 hash1(x)=x mod tableSize(tableSize必须为素数),hash2(x)=R−(x mod R),(R必须为素数)。
这里取tableSize = 10(计算方便),R = 7(小于tableSize 的素数)。首先89存入,下标9的位置没有冲突,直接存入,不计算散列函数2。假设再49插入时计算散列函数1,发现插入位置9发生冲突,需要计算散列函数2,hash2(49)=7−(49 % 7)=7。从9开始,移动7个步长,所以移动到6的位置。

