Songbirds


春

散列函数与分离链接法

  • ~5.91K 字
  1. 1. 5.1 散列
  2. 2. 5.2 散列函数
    1. 2.1. 5.2.1 散列函数实现方案一
    2. 2.2. 5.2.2 散列函数实现方案二
    3. 2.3. 5.2.3 散列函数实现方案三
  3. 3. 5.3 哈希冲突之分离链接法
    1. 3.1. 5.3.1 具体操作

《数据结构与算法分析Java语言描述》第五章5.2与5.3节读书笔记

5.1 散列

  1. 理想的散列是只包含固定大小的数组，

  2. 通常查找是对某个数据域进行的，这部分叫做关键字(key)

  3. 每个关键字按照一定规则，均匀的映射到整个数组中。这个映射叫做散列函数

优秀的散列函数，能够将映射冲突的可能性降低到最小

5.2 散列函数

  如果输入的关键字都是整数，则一般的简单映射函数就是使用key % tableSize，直接取模。同时保证表的大小为素数，是一个好得做法。但是通常得关键字都是字符串。则散列函数有以下方法可以考虑。

5.2.1 散列函数实现方案一

把字符串得ASCII码或者Unicode码的值相加。

1
2
3
4
5
6
7
public static int hash(String key, int tableSize) {
    int hashVal = 0;
    for (int i = 0; i < key.length(); i++) {
        hashVal += key.charAt(i);
    }
    return hashVal % tableSize;
}

  以上函数，实现简单，计算方便，但是如果表很大，则表的的高位利用率较低，导致冲突率增大。
假设表的大小是一个素数：tableSize = 10007，并假设所有关键字至多8个字符(ASCII字符)，则该散列函数只能计算得到 0~1016（127*8）范围内的值。之后对tableSize 进行取余操作，导致1017之后的数是一定取不到的。从而分配不到高位的数组上去。

Java的散列表如HashMap等只会进行扩容，并不会缩小数组，如果采用ASCII码方案，HashMap的数组扩容后，使用不满，可能导致上述的情况发生。

5.2.2 散列函数实现方案二

假设key至少有三个字符，只考察前三个字符，将ASCII码乘起来得到一个整数

1
2
3
public static int hash2(String key, int tableSize) {
    return (key.charAt(0) + 27 * key.charAt(1) + 27 * 27 * key.charAt(2)) % tableSize;
}

  值27表示ASCII字符加一个空格，第一个字符就是本来的值，第二个字符是27 * 原值，第三个字符是27*27*原值。假设在完全随机的情况下，则3个字符的组合有19683种组合的可能。大于tableSize = 10007，则可以均匀分布。但是单词是有一定规律的，并不是均匀分布的。根据统计单词的前三个字母只有2851种组合，所以这种方法还是不适合。

Java的HashMap的数组最大为2302^{30}，如果采用这种方案，最大可能需要所有计算和大于2302^{30}的情况，需要7位的情况。

5.2.3 散列函数实现方案三

所有字符参与计算，计算∑i=0keySize−1Key[i]∗37i\sum_{i=0}^{keySize - 1} Key[i]* 37^i，使用horner法则 计算一个37的n次多项式,37是一个质数。

  根据horner法则计算一个37的多项式：例如：hk=k0+37k1+372k2h_k = k_0 + 37k_1 + 37^{2}k_2，则根据horner法则可以转为：hk=((k2)∗37+k1)∗37+k0h_k = ((k_2) * 37 + k_1)*37 + k_0，可以简化计算复杂度。将其扩展到n项式

1
2
3
4
5
6
7
8
9
10
11
12
public static int hash3(String key, int tableSize) {
    int hashVal = 0;
    for (int i = 0; i < key.length(); i++) {
        hashVal += 37 * hashVal + key.charAt(i);
    }
    hashVal %= tableSize;
    // hashVal可能会存在int溢出的问题，导致为负数，因为取余tableSize后，则hashVal绝对值一定小于tableSize，相加将其变正即可
    if (hashVal < 0 ) {
        hashVal += tableSize;
    }
    return hashVal;
}

  改散列函数基本可用，且实现简单。但是如果关键字特别长，则计算耗时特别多，一个行之有效的方法是只取奇数位置的字符串进行计算。不能只取部分的原因是，例如地址之类的，前半部分都是一样的。

5.3 哈希冲突之分离链接法

将散列到数组同一个位置上的所有元素都保留到同一个列表中。并连接到数组对应下标上的位置(数组中并不存储元素，只存储于列表)

5.3.1 具体操作

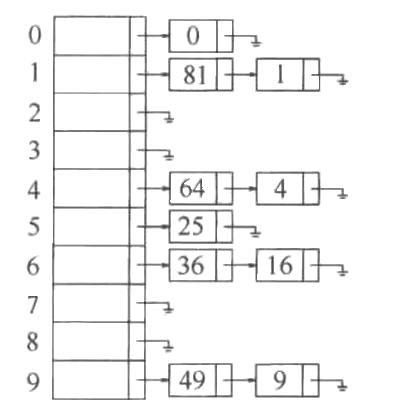
  为简化操作，这里假设关键字是前10个完全平方数，并假设散列函数是hash(x) = x mod 10（表的大小不是素数(是10)，这里是为简化操作）。
分离链接散列表
  先计算出hash，确定应该是数组的哪个下标的位置，然后遍历该下标的链表。如果执行插入，则查看当前插入的元素是否已经在链表上，不在则将值插入到链表头(最近操作的值，在未来的使用概率越大，可以加快查找)。

Jdk8的hashMap从之前的头插法改为尾插法，是为了解决多线程下，hashMap扩容时rehash时导致的链表成环的问题(并发请用correntHashMap)。jdk8及之后改为了尾插法。

  本次实现的对象，必须实现equals方法于hashCode方法。hashCode用来计算判断应该链在哪条链表下，equals用于在hsah冲突后判断是否时同一个对象。如下是一个实现。

链接法的大部分实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
public class SeparateChainingHashTable<AnyType> {

    private static final int DEFAULT_TABLE_SIZE = 101;

    /**
     * List数组,数组的每个位置准出List(链表)，就是之前说的hash表的数组
     * 位置上的链表，就是链接上去的链表
     */
    private List<AnyType>[] theLists;

    private int currentSize;

    /**
     * 无参构造调用有参构造，并设置默认值
     */
    public SeparateChainingHashTable() {
        // this指代本类，类名()就是构造方法
        this(DEFAULT_TABLE_SIZE);
    }

    /**
     * 数组链表的构造方法
     *
     * @param size 数组的长度
     */
    public SeparateChainingHashTable(int size) {
        // 初始化指定长度的链表数组
        theLists = new LinkedList[nextPrime(size)];
        // 给数组上的每一个位置创建链表
        for (int i = 0; i < theLists.length; i++) {
            theLists[i] = new LinkedList<>();
        }
    }

    /**
     * 计算hash值，并计算出应该插入数组上的哪个下标的链表
     *
     * @param x 要计算插入位置的元素
     * @return 要插入位置的下标
     */
    public int myHash(AnyType x) {
        int hashVal = x.hashCode();
        hashVal %= theLists.length;
        if (hashVal < 0) {
            hashVal += theLists.length;
        }
        return hashVal;
    }

    /**
     * 扩容并进行reHash
     */
    private void reHash() {
        List<AnyType>[] oldLists = theLists;
        // new创建的新的list
        theLists = new List[nextPrime(2 * theLists.length)];
        // 创建链表
        for (int j = 0; j < theLists.length; j++) {
            theLists[j] = new LinkedList<>();
        }

        currentSize = 0;
        // 将所有oldList中的元素插入新的List
        for (int i = 0; i < oldLists.length; i++) {
            for (AnyType item : oldLists[i]) {
                insert(item);
            }
        }
    }

    /**
     * 插入元素
     *
     * @param x 待插入的元素
     */
    public void insert(AnyType x) {
        // 获取x应该插入的那个链表
        List<AnyType> whichList = theLists[myHash(x)];
        if (!whichList.contains(x)) {
            whichList.add(x);
            // 每插入一个元素currentSize就会加1，当currentSize大于数组长度后，就会rehash扩容
            currentSize += 1;
            if (currentSize > theLists.length) {
                reHash();
            }
        }
    }

    /**
     * 判断整个数组链表是否包含某个元素
     *
     * @param x 要查询的元素
     * @return true如果包含
     */
    public boolean contains(AnyType x) {
        // 计算在那条链表
        List<AnyType> whichList = theLists[myHash(x)];
        return whichList.contains(x);
    }

    /**
     * 删除元素x
     *
     * @param x 待删除的元素
     */
    public void remove(AnyType x) {
        List<AnyType> whichList = theLists[myHash(x)];
        if (whichList.contains(x)) {
            whichList.remove(x);
            currentSize--;
        }
    }

    public void makeEmpty() {
        for (int i = 0; i < theLists.length; i++) {
            theLists[i].clear();
        }
        currentSize = 0;
    }
}

装填因子λ\lambda：散列表中的元素个数与数组大小的比值

  上例的装填因子λ\lambda=1.0，链表的平均长度为λ\lambda(计算方法如上定义，平均每个列表有多少个元素)，一次平均查找需要1+λ/2\lambda / 2。由此可以得出，表大小对查找效率基本无影响，影响较大的是装填因子。分离散列的一般做法是让λ\lambda = 1，

本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可