floyd判圈算法(龟兔赛跑算法)简介
floyd算法判断链表是否有环
floyd算法计算环的长度
floyd算法寻找环的起点
floyd算法主要基于两个快慢指针,一个慢指针slow,快指针fast。慢指针每次移动1,快指针每次移动2。算法的时间复杂度为O(N)
1 判断是否有环
慢指针每次移动一步,快指针每次移动两步,若fast指向的对象与slow指针指向同一个对象,则说明有环。
证明:反证法:
如果没有环,则slow指针永远不可能追上fast指针,指向同一个对象。(此足以证明有环)
问题2:fast指针会越过slow指针不相遇吗?从而增加时间复杂度?
不可能。假设fast越过slow,则slow = k + 1, fast = k + 2, 从而错过,往前推一步可知,他们必定在k的位置相遇。
时间复杂度:O(N),在慢指针未走完一圈的时候,快慢指针必定能相遇。(如果无环,则O(N)不必证明)
证明:
- 快指针quick入环。之后,经过一段步骤,慢指针到达环的起点,准备入环。
- 此时,假设快指针距离慢指针x,如果在起点相遇,则x=0
- 设环的周长为L,那么之后就是快指针追赶慢指针,追赶距离为L-x
- 快指针的速度为每次2个距离,慢指针为每次一个距离,则快指针每次追赶2-1个距离,那么需要追赶(2-1) * (L-x) = L-x步。
- 在追赶L-x步的时间里,慢指针走了L-x的距离,由于x>=0,所以在慢指针最多走完一圈(L)的距离时,必定已经相遇。
202. 快乐数 - 力扣(LeetCode)、(287. 寻找重复数 - 力扣(LeetCode))
如果是快乐数,则最后会变为1,如果不是,则会进入几个数的循环。因此不为1时,判断是否有环即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public boolean isHappy(int n) {
int slowNum = n;
int quickNum = getNextValue(n);
while (quickNum != slowNum) {
slowNum = getNextValue(slowNum);
quickNum = getNextValue(getNextValue(quickNum));
}
return quickNum == 1;
}
public int getNextValue(int num) {
int res = 0;
while (num > 0) {
res += (num % 10) * (num % 10);
num = num / 10;
}
return res;
}
}
|
2 求环的长度
当slow和fast相遇后,slow和fast必定在环上,只要让其中一个不动,另一个继续走,并计数,直到两者再次相遇,则可以得到环的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public boolean circleLen(int n) {
int slowNum = n;
int quickNum = getNextValue(n);
while (quickNum != slowNum) {
slowNum = getNextValue(slowNum);
quickNum = getNextValue(getNextValue(quickNum));
}
int len = 1;
slowNum = getNextValue(slowNum);
while (slowNum != quickNum) {
slowNum = getNextValue(slowNum);
len++;
}
return len;
}
public int getNextValue(int num) {
int res = 0;
while (num > 0) {
res += (num % 10) * (num % 10);
num = num / 10;
}
return res;
}
}
|
3. 求环的起点
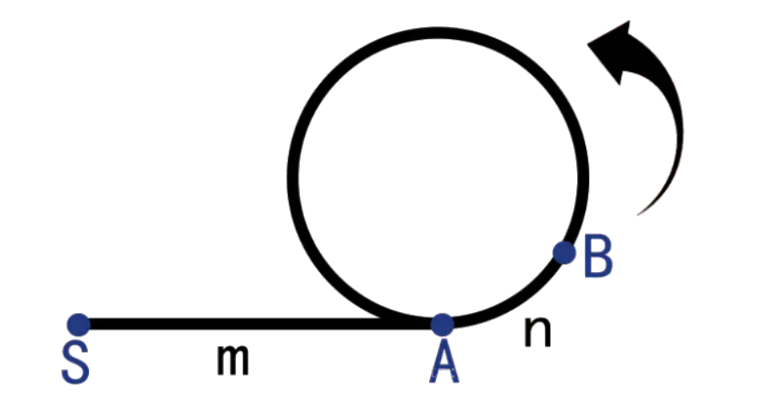
如图为一个有环链表,对于该链表有如下定义:
- A为环的起点,S为链表的起点,B为slow与quick指针相遇的点。m为S到A的距离,n为A到B的距离
- slow指针走过的所有节点为i,则quick指针必定走过节点2i。因为quick的速度是slow的2倍。
则有:
- 对于slow指针:i = m + n + aL (a为slow走过环的圈数,L为环的节点总数)
- 对于quick指针:2i = m + n + bL (b为quick走过的圈数,L同上)
- 第2点 - 第1点则有:i = (b-a)L, 则i 必定为L的整数倍。
- 带入第1点则有:m + n = (b - 2a) L,则m + n 必定为L的整数倍(b, a为整数,且m+n > 0, 所以有 b-2a > 0),m+n是一个完整的环。
- 所以当从B点继续走m步,则必定停在A点(因为4,m+n是一个完整的环)。
- 但是m是多大,不清楚。此时,只需要一个指针从S点出发,另一个从B出发。如果走了m,S必定到达A点,B也必定到达A点,则当两个指针第一次相遇的时候,就是起点A。我们就不需要处理m的问题了。
142. 环形链表 II(LeetCode)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head== null || getNext(head) == null) {
return null;
}
ListNode slowNode = getNext(head);
ListNode quickNode = getNext(getNext(head));
while (slowNode != null && quickNode != null && getNext(quickNode) != null && getNext(getNext(quickNode)) != null && slowNode != quickNode) {
slowNode = getNext(slowNode);
quickNode = getNext(getNext(quickNode));
}
if (quickNode == null || getNext(quickNode) == null || getNext(getNext(quickNode)) == null) {
return null;
}
slowNode = head;
while (slowNode != quickNode) {
slowNode = getNext(slowNode);
quickNode = getNext(quickNode);
}
return quickNode;
}
public ListNode getNext(ListNode node) {
return node.next;
}
}
|
注:此题也可以用哈希表做,用一个指针遍历,将走过的节点存储起来,如果有环,则哈希表中必定能找到这个点,并且第一次找到的点就为起点(因为环的起点在前面)。如果到达节点末尾,则说明无环。
哈希表的时间复杂度也是O(N),但是空间复杂度为O(N),floyd判圈的空间复杂度为O(1)。
