B-Tree

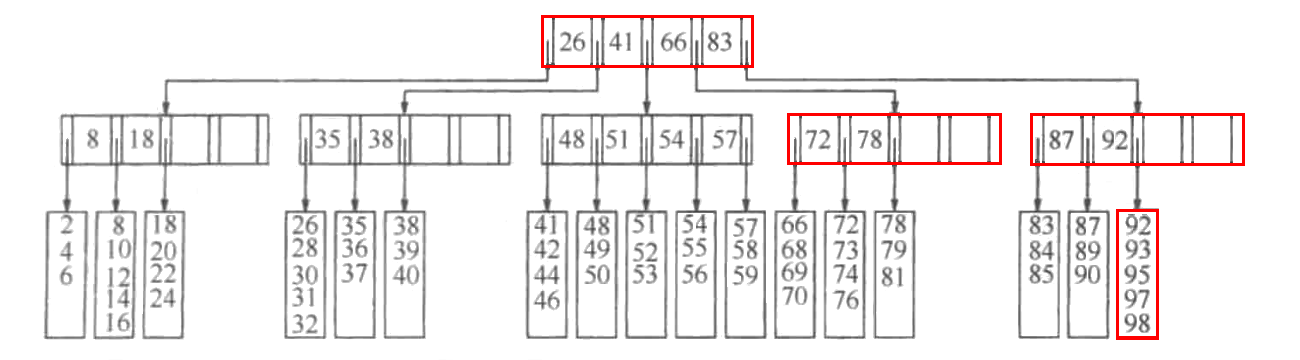
B树概念简介，无代码实现

  之前的各种二叉树都是存储在内存中的，而如果数据量过大，则需要将数据存储在磁盘中。然而磁盘的读取(I/O)速率相比内存而言较为低下。即使是AVL树，平均查找为时间为$logN$，对于1千万的数据，则大约需要24次对磁盘的访问。

4.7 B-Tree

  B树是一棵自平衡的多路平衡查找树，一棵的M叉B树的最坏查找时间复杂度为$log_{\frac{M}{2}}{N}$。M(叉)阶B树具有如下特点：

1. 所有数据都存储在树叶上，(其他节点只承担索引的作用)。
2. 非叶子节点，存储最多M-1个关键字(索引)
3. 如果根不是叶子节点，则根的子节点为[2, M]个
4. 每个非叶子节点的子节点个数在[M/2, M]个，向上取整。
5. 所有叶子节点都在同一高度。
6. 所有叶子节点具有[L, L/2]个数据项(L不一定=M )

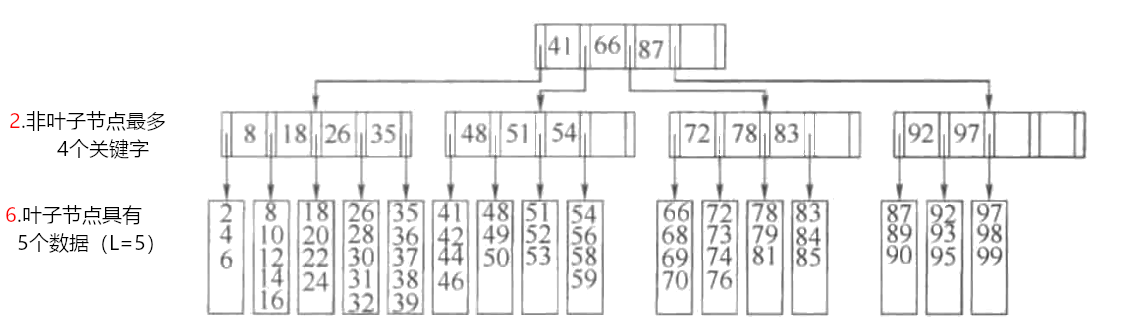
4.5.1 B树的插入

  若树叶没有满的情况下，直接插入即可。较为复杂的插入情况：

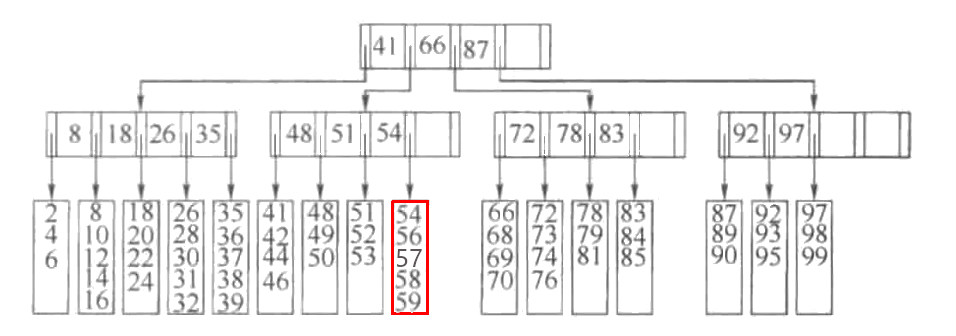
1、叶子满但能够分裂

  值55想要插入下图，该树叶已满，此时在满足树叶具有[L, L/2]的情况下，可以将树叶平均分裂成两个树叶后插入。这种插入变化情况是较少的。因为一次插入，就能保证下L/2次不会分裂。

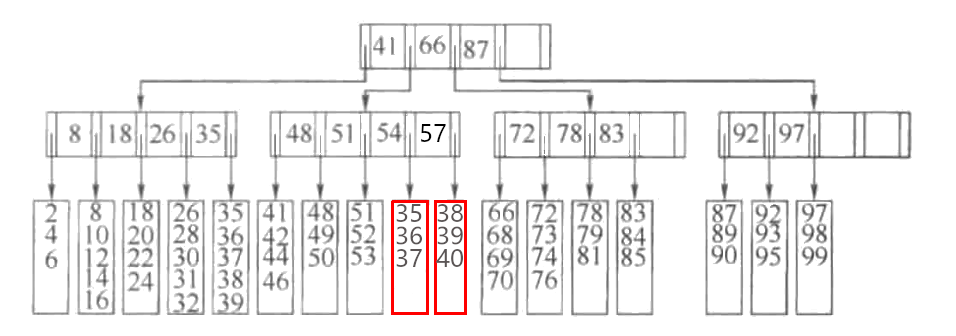
2. 叶子满不能分裂父分裂

  值40想要插入时，插入位置树叶已满，同时父节点也已满（节点上最多具有M-1个个索引），可以将父节点分裂。（如果分裂后，父父节点满，则同时继续向上分裂），如果继续分裂到树根，如果继续分裂，则会的到两个树根，此时只能将树根分裂，并给他们建立一个新的树根（这是允许树根只有两个子节点的原因）。
  这是B树增加高度的唯一方式。

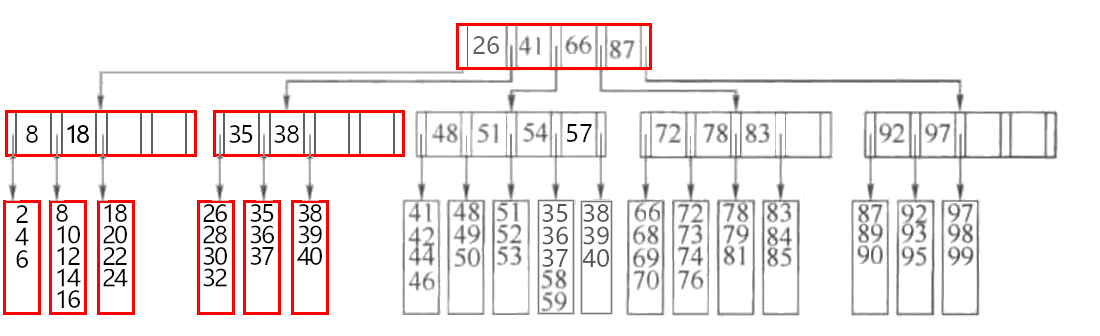
4.5.2 B树的删除

1. 删除后可以从兄弟节点借

  如果叶子节点的值删除后，节点数量值小于L/2，但是相邻兄弟节点大于L/2，则可以从兄弟节点借。

2. 删除后与兄弟节点合并

  兄弟节点也只有L/2，那么可以和兄弟节点合并，同时父节点会失去一个儿子。如果父节点失去子节点后也少于，则向兄弟节点借，如果不行，则继续与兄弟节点合并。。。，如果这个操作进一步导致根只有一个子节点，那么删除根，并让这个子节点作为根。
  这是B树降低高度的唯一方式。