伸展树(Splay)

伸展树简介

4.5 伸展树

本质是一颗二叉查找树，在查找后，通过AVL的旋转操作，将查找的那个节点，旋转到root节点位置，达到将经常查找的节点置于root节点附近的目的，减少查询次数。

  伸展树保证从空树开始连续M次对树的操作最多花费$O(M \log N)$，但是不保证最坏的情况下时间复杂度为$O(\log N)$，m次伸展操作的均摊时间效率$O(M \log N)$。
  即使只读访问，每次访问后，其结构也会发生变化，因此在多线程下，其需要额外的维护。

4.5.1 一个简单的伸展想法

  假设我们想查找的是k1，则从k1开始，自底向上的去操作，每次和他的父节点进行单旋转，将k1旋转上去(这个操作会将k1的父节点旋转下来，k1旋转上去)，直到将k1旋转到root节点。这样的操作虽然可以将k1旋转上去，但是其会将以前比k1靠近root的节点推到k1之前那么深，违背了最近查找节点置于顶部的逻辑。

4.5.2 正确的伸展

   正确的旋转，是每次旋转都基于AVL的旋转操作，将查找节点K1旋转到root节点。主要基于以下两种操作

1. zig-zag(之字形)
   
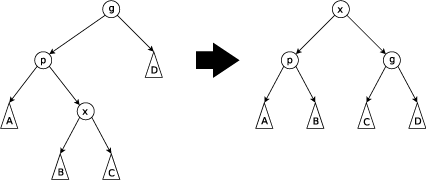
   要将x旋转上去，g、p、x组成之字形，先将x旋转到p上，再将x旋转到根节点即可。

2. zig-zig(一字型)
   
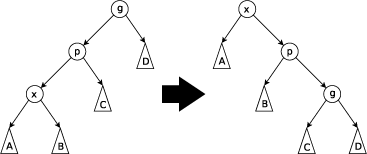
   g、p、x组成一字型，先将p旋转上去，再将x旋转上去即可。

3. 实例：
   使用如下示例，对k1进行操作：
   示例原图：
   

   进行一次zig-zag旋转：

   

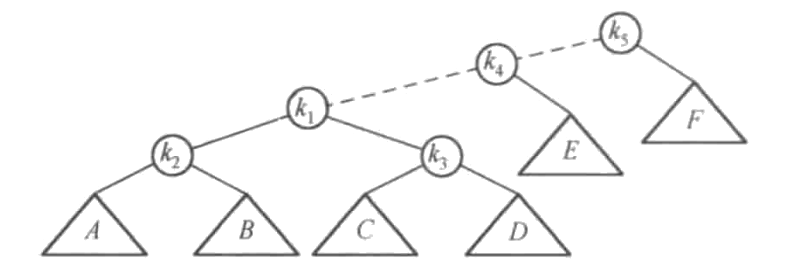
   进行一次zig-zig旋转：
   

   4.5.3 自顶向下的伸展树

      在自底向上的伸展树中，我们需要求一个节点的父节点和祖父节点，在实现的过程中需要使用栈来保存访问路径进行回溯，这种伸展树难以实现，自顶向下可以只使用O(1)的存储方式，实现一样的效果。

   TODO : 该章节为书本第十二章实现，暂定之后实现