树与二叉树

《数据结构与算法分析Java语言描述》第二章4.1与4.2节节读书笔记

4.1 树

定义树的一种自然方式是递归。一棵树是N个节点和N-1条边的集合。

一棵树是一些节点的集合。可以是空集。若不为空，则由根节点r和0个或多个非空的字树T1，T2，T3，…，Tk组成，子树中每一颗根都被来自r的一条有向边连结。

树的术语定义：

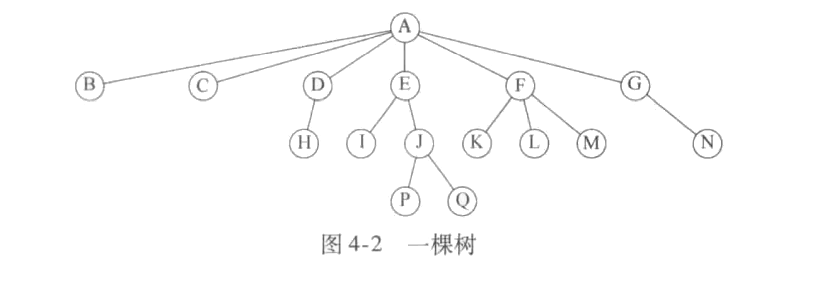
• 子节点：若节点E有子树，则子树的根节点(如J)为E的子节点。
• 父节点：若节点E有子节点，则E为子节点(如J)的父节点。
• 节点的度：节点有子树棵树(子节点个数)
• 叶子节点：没有儿子节点的节点(度为0的节点)，如图节点P等。
• 兄弟节点：具有相同父节点的节点互为兄弟节点。如P节点与Q节点。
• 节点层次(level)：本书称节点$n_i$的深度，从根节点到$n_i$的路径长，因此根节点层次(深度)为0.
• 树的深度(注意是树)：其他书特指：根节点到最远叶子节点的路径长。根节点深度为0。
• 树的高度：最深的叶子节点高度为0，一棵树高等于根高。如E：深度为1，高为2。(其他书特指最大高度。即高度=深度)。
• 祖先与真祖先、后裔与真后裔：如果存在$n_1$到$n_2$的一条路径，那么$n_1$为$n_2$的祖先，$n_2$为$n_1$的后裔，如果$n_1 \ne n_2$则$n_1$是$n_2$的真祖先，$n_2$是$n_1$的真后裔。

4.1.1 树的实现

  节点存储数据，另有一些链，该节点的每一个子节点都有链指向它。由于不确定有多少链，因此采用其他解决方法，将每个节点的子节点都放在一个链表中。
  如下是针对上述的一种实现(对应图4.2)。向下的箭头指向firstChild(第一儿子)的链，水平箭头指向nextSibling(下一兄弟)的链。null链未画出。如节点E有链指向兄弟F，另一链指向儿子I。

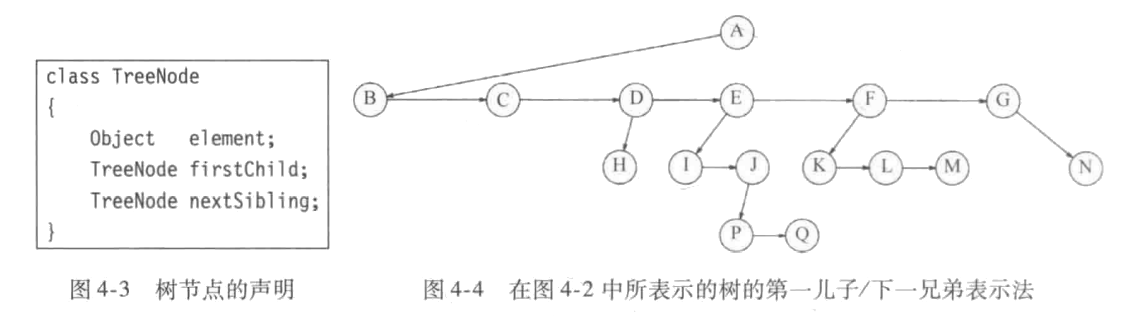
4.1.2 树的应用与遍历

所谓的序是指遍历时根的位置，如前序就是根左右，中序就是左根右(针对二叉树)，后序就是左右根

树的应用
  多叉树的一种用法是UNIX与DOS系统的目录结构，如下图是UNIX文件的一个典型应用。

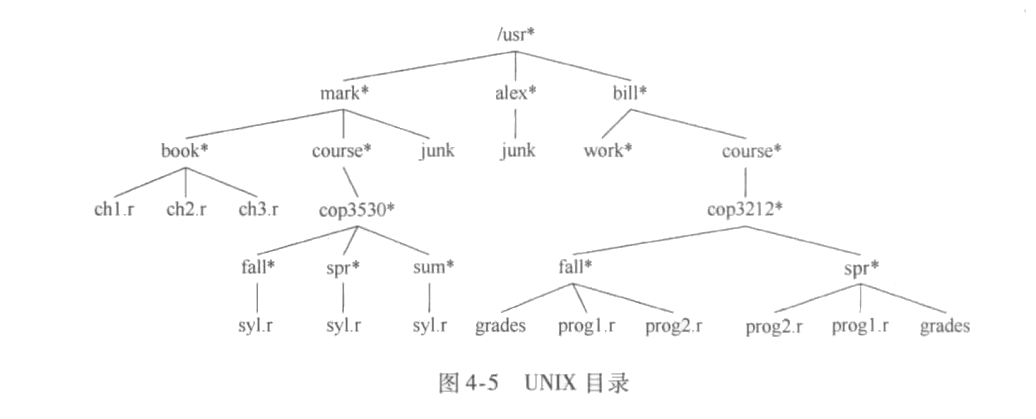
先序遍历展示所有目录：
  先序遍历按照先根后左(子树)再右(子树)。例如上图某次的遍历实现。usr -> mark -> book - > ch1.r -> ch2.r -> ch3.r -> course(右子树) -> cop3530 -> fail -> syl.r -> spr -> syl.r -> sum -> syl.r -> junk(右子树) -> alex…
该算法遍历每一个节点，显然先序遍历的时间复杂度为O(N)。
  记忆口诀：根左右

1
2
3
4
5
6
7
8
9
10

// 伪代码实现，具体实现会在二叉树实现
// depth 从深度为几的位置开始遍历，如要遍历所有数据，从depth = 0开始
private void listAll(int depth) {
    print(depth); // 打印文件或文件夹名字
    // 遍历该目录下的所有子文件目录，再里面递归遍历
    for each file c in this directory (for each child) {
        // 递归遍历所有子目录的结果
        c.listAll(depth + 1);
    }
}

后序遍历计算某树目录下的所有文件大小：括号内代表所占区块个数

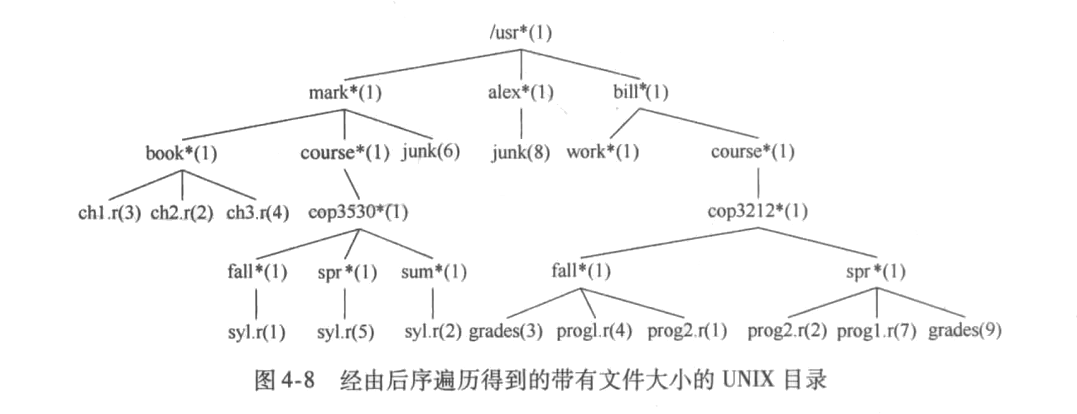
  要计算usr目录下的文件所占的存储大小，找出其所有子目录mark(30)、alex(9)、bill(32)的区块个数和为71，加上usr的区块个数和为1，最终为72。如果当前对象不是目录，size只返回当前对象的区块数，否则该目录占用的区块数被加到所有子节点(递归)发现的区块数中。usr:1(暂存) -> chl.r:(3+1) -> ch2.r(4+2) -> ch3.r(6+4) -> book(10+1) -> syl.r(11+1)…
注意：以上暂存代表并未实现真正的遍历，因此遍历是从ch1.r开始的，ch1.r -> ch2.r -> ch3.r -> book -> syl.r -> fall -> syl.r -> spr -> syl.r -> sum -> cop3530 -> course -> junk -> mark -> junk -> alex ->work -> grades…
  记忆口诀：左右根

1
2
3
4
5
6
7
8
9
10
11
12

// 后续遍历伪代码实现 计算总区块数
public int size() {
    // 当前目录所占区块数
    int totalSize = sizeOfThisFile();
    if (isDirectory) {
        for each file c in this directory (for each child) {
            // 总区块数=当前子树根目录区块数+其下所有区块数总和
            totalSize += c.size();
        }
    }
    return totalSize;
}

4.2 二叉树

如果一棵树，其每个子节点最多不超过两个儿子。在最坏的情况下二叉树可能会退化为一个链表

4.2.1 二叉树的实现

  一棵二叉树最多有两个节点，因此只需要一个元素的信息(element)和到其他两个节点的引用(left与right)组成。

1
2
3
4
5

Class BinaryNode {
    Object element;		// 当前节点数据
    BinaryNode left;	// 左孩子
    BinaryNode right;	// 右孩子
}

4.2.2 例子：表达式子树

  如下图为一个表达式子树，树叶为操作数，其他节点为操作符，其操作都是二元的，(如果不是，孩子可能出现大于2的情况)。

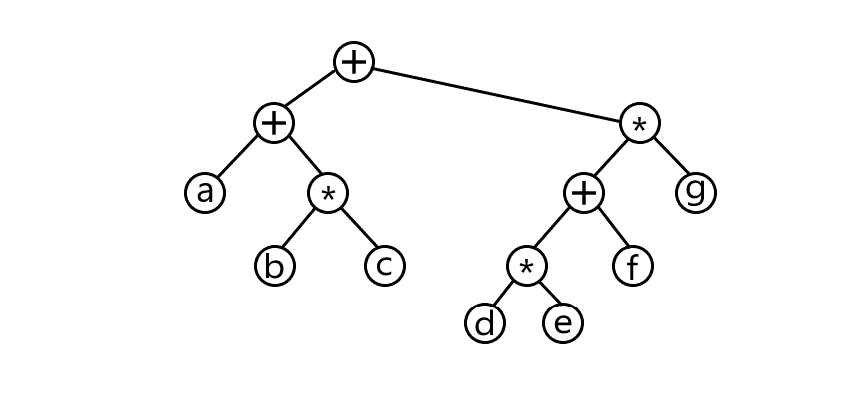
中序遍历：如树的介绍左根右，递归产生带括号的左表达式，然后打印出再根的运算符，再递归产生一个带括号的有表达式，从而得到带括号的中缀表达式(一个括号代表一个子树)。得到：$(a + b * c) + ((d * e + f) * g)$。中缀表达式。
后序遍历：如树介绍的左右根，先递归的打印出左子树，右子树，再打印运算符，将的到$a \ b \ c \ * \ f \ + \ g \ * \ +$ 。后缀表达式(逆波兰表达式)。
先序遍历：如树介绍的根左右，先打印出运算符，再递归打印出左子树和右子树。得到$++a*bc*+*defg$ 。前缀表达式(波兰表达式)。